Manuel Feito Guzmán

Las Otras Matemáticas
(Textos para todos los públicos)

Textos en inglés

Presentamos a continuación textos en inglés con más curiosidades, anécdotas, historias, aplicaciones de las matemáticas a otras disciplinas y cuestiones que a día de hoy aún permanecen abiertas. Esta selección de textos puede constituir un recurso valioso para trabajar con estudiantes en Programas Bilingües.

26. Millennium Prize Problems or how to get a million dollars

The Millennium Prize Problems are seven problems in the field of Mathematics stated in 2000. These are old problems. Nowadays, six of the seven problems remain unsolved. A correct solution to any of them would result in a million dollar prize. $1,000,000 is about 900,000 euros.

The only solved problem is the so-called Poincaré conjecture (now called Poincaré theorem as it has already been proven). It was originally posed in 1904 by the French mathematician Henri Poincaré, and was only solved a century later by the Russian mathematician Grigori Perelman. He was awarded the $1,000,000 prize in 2010... but he declined the award! (wow!)

Perelman also declined the Fields Medal, which is one of the most relevant prizes in Mathematics (there is no Nobel Prize in Mathematics). He said:

Everybody understood that if the proof is correct, then no other recognition is needed. I'm not interested in money or fame.

The Fields Medal is granted every four years on the occasion of the International Congress of Mathematics to recognize outstanding mathematical achievement. The medal is made of gold and shows the face of the brilliant Archimedes (§34). Contrary to other prizes that are usually awarded to senior scientists, the Fields Medal can only be won by mathematicians under the age of 40. This may sound strange, but remember that most important discoveries are made by young men and women with a great scientific creativity (which tends to decrease with age).

Another hard-to-solve problem was Fermat's Last Theorem, which was indeed a conjecture for almost 400 years until the British mathematician Andrew Wiles solved it. He first attempted to give a valid proof in 1993, when he was 40, but there was a little mistake that he could not correct until 1995. By then he was 42, past the limiting age to receive the Fields Medal! Nevertheless, the International Mathematical Union gave him a silver plaque in recognition for his proof.

To conclude, here you have the list of the 6 millennium problems that remain unsolved' just in case you want to try to win a million dollars (and surely a Fields Medal).

• The Riemann hypothesis (§8)
• Yang-Mills Theory and the Mass Gap Hypothesis
• The P vs. NP problem (§17)
• The Navier-Stokes Equations
• The Birch and Swinnerton-Dyer Conjecture
• The Hodge Conjecture

27. Cheryl's birthday problem goes viral

SASMO stands for "Singapore and Asian Schools Math Olympiad". According to its webpage it is an organization devoted and dedicated to bringing a love of Mathematics to students. It concerns itself with interest and enthusiasm for mathematical problem solving, developing mathematical intuition, reasoning and logical thinking, as well as creative and critical thinking. The following problem, aimed at students between 14 and 16, was proposed by SASMO and quickly went viral. It is known as Cheryl's birthday problem.

Albert and Bernard just became friends with Cheryl, and they want to know when her birthday is. Cheryl gives them a list of 10 possible dates:

May 15, May 16, May 19,

June 17, June 18,

July 14, July 16,

August 14, August 15, August 17.

Cheryl then tells Albert and Bernard separately the month and the day of her birthday respectively.

Albert: I don't know when Cheryl's birthday is, but I know that Bernard doesn't know too [sic, although better grammar would be 'either' instead of 'too'].

Bernard: At first I don't [sic] know when Cheryl's birthday is, but I know now [sic, but better grammar could be: 'At first I didn't know when Cheryl's birthday is, but now I do'].

Albert: Then I also know when Cheryl's birthday is.

So, when is Cheryl's birthday?

It could seem impossible (§1, §4, §30) to solve the problem with apparently no information provided, but it isn't if you are used to these kind of problems. However, if this is the first time you are facing one of these, it is likely that you have to think about it for a long time. I hope you enjoy it.

You got it? OK, here you have the key points that you should have followed in your reasoning:

• Albert's first comment eliminates all the dates of May and June. Can you see why?
• Bernard's following comment eliminates July 14 and August 14.
• Albert's last comment eliminates August 15 and August 17.

So the final answer is... exactly, the remaining date you thought, didn't you?

28. Pixels, bits, and steganography

Each single point in a digital image is called a pixel. An image is composed of so many pixels that you cannot distinguish them unless you zoom in the image. Only after a great magnification you are able to see squares of different colors. Each of these colored squares is a pixel.

Computers use the RGB model to specify a color. RGB stands for Red, Green, and Blue. The combination of these three colors -called channels in computation language- can produce any other color. So, for coloring a pixel, the proportion of red, green, and blue must be specified.

Computers use an 8-bit scale from 0 to 255 for each channel. In other words, there are 2⁸ = 256 different intensities for each of the three basic colors. The greater the number, the brighter the color. By combining the three channels you can create up to 256×256×256 = 2⁸×2⁸×2⁸ = 2²⁴ colors. That's more than 16 million colors! Here are some examples:

Color	Name	(R,G,B)
	red	(255,0,0)
	yellow	(255,255,0)
	light blue	(135,206,250)
	black	(0,0,0)
	pink	(255,192,203)

But computers prefer to only use 0's and 1's instead of numbers up to 255. That's not a problem because every natural number can be written as a binary number, i.e. using 0 and 1 (by the way, that's a bit). For instance the values for each channel in the light blue of the image above are indeed

(135, 206, 250) = (10000111, 11001110, 11111010)

Thus, one of these light blue pixels would correspond to the previous long string of 24 bits.

We have written in bold the so-called least significant bits, which are the right-most digits for each channel. They are said to be "least significant" because swapping 0 and 1 in those positions does not alter the color appreciably: it is like changing just one unit over 256 in the channels.

We are almost done! Now we can erase the least significant bits of a photo and write instead the binary string for a secret message. For example to hide the message "HELLO WORLD" in a digital image, we must do the following:

1. Associate the letters H-E-L-L-O-W-O-R-L-D with numbers, as done for instance in the usual ASCII convention, based on which a unique binary string corresponds to each letter:

H=01001000; E=01000101; L=01001100; O=01001111; W=01010111; R=01010010; D=01000100

So our "HELLO WORLD" would read:

01001000 01000101 01001100 01001100 01001111 01010111 01001111 01010010 01001100 01000100

2. Choose a beautiful digital picture and overwrite the first non significant bits of your photo with the previous string. Nobody will notice that you have substituted a bunch of pixels by others with almost the same color.

This practice of concealing a message within a digital file (such as a digital image) is called steganography. And it is a quite common method to transfer information used by intelligence services and terrorist groups.

Do you find it difficult to implement? It is not. As a matter of fact there are many tools on the Web to do it. Just choose a photo and insert a text in it. Run the software and voilà.

The odds of someone finding your secret message are very rare, but take into account that steganography is not a cryptography method (such as the one-time pad used by Che Guevara and Fidel, §20). This is because the message is not ciphered, although you could do it before you hide the message inside the 0's and 1's of the digital file (only for paranoids!).

29. Goldbach's conjecture

Goldbach's conjecture is one of the oldest unsolved problems in mathematics. It states:

Every even integer greater than 2 can be expressed as the sum of two primes.

(Remember that a prime is a natural number greater than 1 that has no positive divisors other than 1 and itself. The first prime numbers are 2, 5, 7, 11, 13, 17, ...)

For the first even numbers, Goldbach's conjecture reads:

• 4 = 2 + 2
• 6 = 3 + 3
• 8 = 3 + 5
• 10 = 3 + 7
• 12 = 5 + 7
• 14 = 7 + 7
• 16 = 5 + 11

For some numbers there is more than one way to express them. For instance, the number 10 can be written as 3+7, but also as 5+5.

Mathematicians believe that Goldbach's conjecture is always true for any even number greater than 2. Christian Goldbach and Leonhard Euler (§36) thought the same in 1742, when they proposed the conjecture. Euler wrote:

I regard it as a completely certain theorem, although I cannot prove it.

Nowadays, it remains unproven. For every even number up to 4,000,000,000,000,000,000, modern computers have checked it, but that is not enough, as there are infinitely many numbers. So, there are two options to solve the problem:

1. Find an even number that cannot be expressed as the sum of only two primes. (That's unlikely. Mathematicians believe there is no such a number)
2. A sophisticated mathematical reasoning (§3, §11) to ensure that the conjecture is true for EVERY even number greater than two.

30. Parrondo's paradox: Two bad things becoming a good one

Game theory is an important branch of Mathematics strongly linked to gambling. Mathematicians say that a "losing game" is one in which you tend to lose on average. All the games played in casinos are losing games (otherwise it wouldn't be a business for the house). But sometimes the unexpected happens: Two different losing games played back and forth can surprisingly result in an averaged positive outcome!

This counterintuitive result became popular after a paper published in the journal Nature by G.P Harmer and D. Abbott. The authors were inspired by the ideas originally presented by the Spanish physicist J.M. Parrondo in a conference in 1996. His seminal idea was the translation of a well-known problem in Physics -the induction of directed motion through the rectification of stochastic thermal fluctuations, so-called Brownian motors or ratchets (err... what?)- into the language of game theory.

All right, let's define the two losing games, say Game A and Game B.

First, Game A. Consider tossing a coin. Getting 'heads' you win 1 euro, getting 'tails' you lose 1 euro. With a fair coin, heads come up with a probability of 0.5 (that is, 50%), and tails come up with the same probability. Statistically you can play that game with no significant profit or loss of money in the long run. But now, suppose that the coin is designed to fall with slightly greater probability as 'tails': for instance, 0.505. With this biased coin you will lose in average. In fact, the more you play, the more money you lose. You'll finally be penniless. Well, this is our losing Game A.

Now let's define Game B. This time the player gambles on a slightly more complex game involving two coins (Coin '1' and Coin '2'). Coin 1 is biased so it gives you odds of winning at 0.745 (that means your chance of winning is almost seventy-five percent). Well, this is in fact a really good coin for you... but all that glitters is not gold because there is also Coin 2 in Game B, which is an awfully unfair coin with only a probability of 0,095 for you to win (less than a one-tenth chance of winning). When do we have to toss the good Coin 1 and when do we have to toss the bad Coin 2? In Parrondo's original game -there are many variants- Game B depends on the capital. If your total money is a multiple of three (you know, 0?, 3?, 6?, 9?, 12?...) you have to flip Coin 1; if it is not, you are forced to toss the bad Coin 2. Not only is Coin 2 really bad (while Coin 1 is only slightly good), but also you would play against bad Coin 2 more times (because there are two times as many non-multiples of three than there are multiples of three). Game B is definitely a losing game!

Note that the apparently weird values for the probabilities given here (0.505, 0.745, 0.095 ) can be written in terms of a parameter ε=0.005 in a clearer way as 1/2+ε (for Game A), 3/4-ε (for Coin 1 of Game B), and 1/10-ε (for Coin 2 of Game B). Anyway, these particular values can be changed giving similar results, so don't worry about the specific numbers.

Although both Games A and B are losing games, it turns out that playing two rounds of Game A followed by two of Game B (and so on) actually produces a steadily increasing capital. That's Parrondo's paradox. Surprisingly, playing two bad games alternatively results in a good thing! Furthermore, the Parrondo's paradox is also true when the games are switched at random! You would become multimillionaire with that simple strategy.

31. Focus on Math: The ultimate guide to f-numbers in digital cameras

A Digital Single-Lens Reflex (DSLR) camera is a photographic camera that has two parts: a digital imaging sensor in the body of the camera and an objective or lens, which is an optical system that gathers the light to the sensor. We will focus on the lens (sorry for the play on words!) But first, a couple of basic widely-known concepts by photography lovers.

First one: The focal length. It is a measure of how strongly the system converges light. The longer the focal length (e.g. 300 mm), the higher the magnification of the image. Conversely, shorter focal lengths (e.g. 24 mm) lead to lower magnification. When you zoom in and out you change the focal length.

The second concept to keep in mind is the entrance pupil of an optical system, which is closely related to the size of the physical aperture or diaphragm of the camera. In fact, the only difference between the entrance pupil and the physical aperture is the presence of lenses in front of the latter, which effectively modify the size of the image. The effective aperture is the apparent diameter of the diaphragm opening in the camera lens as seen through the front of the lens, and it is measured in mm.

The ratio of these two lengths -the focal length and the effective aperture- is the so-called f-number or f-stop. It is represented by the letter N (not f, be careful!), while the letter f is used to represent the focal length. D stands for the diameter of the pupil entrance.

N = f/D

Note that the f-number is dimensionless. In DSLR cameras you can independently choose the values for N and f, so you are indirectly fixing the effective aperture D according to

D = f/N

For instance, if you have zoomed in to a focal length of f=200 mm and you have set the f-number to N=8 (which is labeled in cameras as "f/8"), then the diameter of the pupil entrance is D=f/N=200/8=25 mm.

One could argue that the diaphragm of a camera lens is not a circle of a diameter D, but a regular polygon delimited by blades. The area of a regular polygon is calculated by multiplying its perimeter (which is the sum of the lengths of all its sides) times the apothem (which is the distance from the center to the midpoint of one of the sides), and then dividing the result of the multiplication by 2. Both the apothem and the perimeter of a regular polygon are directly proportional to its radius (which is defined as the distance from the center of the regular polygon to a vertex), so the area itself is proportional to the square of the radius, thus to the square of the diameter -twice the radius-), as happens with the area of a circle. So... we are not going to make a fuss about whether the pupil entrance is a perfect circle or not, OK? It doesn't matter for our reasoning.

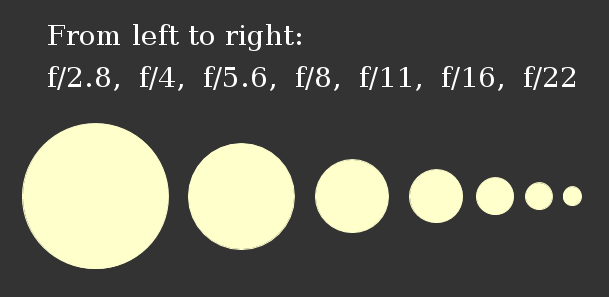
In the vast majority of camera lens you don't change the aperture continuously (you do it when it comes to the pupils of your human eyes). In fact, only certain values of the f-number are allowed in most cameras: f/2.8, f/4, f/5.6, f/8, f/11, f/16, and f/22. Why those weird values? Photography enthusiasts know the answer: they are chosen so that each value in the series allows half of the intensity of light pointing to the sensor as compared to the previous value. But... why is this (approximately) true? Because the area of the aperture corresponding to each of these numbers is half of the corresponding to the preceding value.

If we call A₀ the area for a certain aperture, say f/2.8 for instance, and A₁ the area for the succeeding f-number, say f/4, we impose the condition:

A₀=2A₁

In terms of the diameter D it would read

D₀²=2D₁²

and taking the square root:

D₀=?2 D₁

Therefore, the f-numbers form a geometric sequence with common ratio ?2. If the first term is 1, next ones are

2 = 2, (?2)³ ? 2.8, (?2)⁴ = 4, (?2)⁵ ? 5.6,

(?2)⁶ = 8, (?2)⁷ ? 11, (?2)⁸ = 16, (?2)⁹ ? 22

Some digital cameras allow to change the f-number with more precision, being the possible values 1.0, 1.1, 1.2, 1.4, 1.6, 1.8, 2, 2.2, 2.5, 2.8, 3.2, 3.5, 4, 4.5,5.0, 5.6, 6.3, 7.1, 8, 9, 10, 11, 13, 14, 16, 18... Now, each step that halves the light is subdivided in three. In other words, the new common ratio k of the latter geometric sequence satisfies the condition k³=?2. Solving for k, the ratio is the sixth root of 2, i.e., 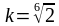, and the above numbers are approximations to the sequence {kⁿ}, being n an integer number. For instance,

k¹² = 4

k¹³ ? 4.5

k¹⁴ ? 5

k¹⁵ ? 5.6

In addition to the aperture, in DSLR cameras you can control the amount of light that reaches the sensor by varying the exposure time (sometimes called the shutter speed), that is, the seconds (or fractions of second, indeed) during which the sensor is exposed to light. Standard values in cameras for the exposure time are: 1/1000 s, 1/500 s, 1/250 s, 1/125 s, 1/60 s, 1/30 s, 1/15 s, 1/8 s, 1/4 s, 1/2 s, 1 s... (s stands for second.) Note that each fraction is roughly half of the previous fraction, so the amount of light that reaches the sensor doubles at each increment step of the exposure time.

Doubling the exposure time and the f-number at the same time does not alter the overall exposure of the photo. This is because the gain in light due to longer exposure time is compensated by the loss of half of the light due to a greater f-number (lower aperture). Thus, once the total amount of light is fixed to ensure a proper exposition (not too dark, not too burn), photographers play with the different pairs of values (f-number, shutter speed) that are equivalent in terms of light gathered, but different when it comes to effects such as sharpness, depth of field, diffraction, motion blur, noise, etc. These artistic effects can also be fully explained mathematically and physically... But that is out of our scope, sorry.

32. Borges, his mother, and a pair of hands with 60 fingers

The Argentinean writer J. L. Borges was one of the most erudite authors of the 20th century. Having a broad knowledge of almost everything, he was particularly interested in some aspects of logic and mathematics, such as the set theory and the idea of infinitum. At his mother's funeral, a friend of the family commented that it was a pity that the poor woman wouldn't be able to reach the age of 100 (she died at the age of 99). It is said that Borges answered:

"I see, Madam, that you are a devotee of the decimal system"

Borges was right: we tend to overestimate the decimal system (based on number 10). From a vital point of view there is not much difference between 99 and 100. But for some reason, we, humans, are in love with round numbers such as 100 or 1000. Our behavior is understandable as we generally use the decimal system. We have 10 fingers, so our tendency to this number is logical. Surely you have seen a child learning to add. They use their hands constantly.

But sometimes we use other numeral systems. For example, the sexagesimal system (based on number 60) is the favorite when it comes to time. So, 1 hour equals 60 minutes instead of 10 or 100 minutes. Why? Well, we inherited the sexagesimal system from ancient cultures -Babylonians were really experts- One important strength of the number 60 is that it has many divisors: it can be divided evenly by 1, 2, 3, 4, 6, 12, 15, 20, 30 and 60.

In addition, it is possible to count up to 60 using your hands in a simply way. Firstly, use your right hand thumb to count up to 12 (see picture below). Then, use the remaining 5 fingers of your left hand to carry how many dozens you have: 1 dozen (12), 2 dozens (24), 3 dozens (36), 4 dozens (48), and 5 dozens (60).

Anyway, I have to confess that I love both numeral systems: living healthy for 100 years (ten times ten) would not be so bad, but 120 years (two times sixty) would be superb!

33. Twin primes: How many

A prime number is a number that cannot be divided by other numbers than itself and the number 1. Here is a list of the prime numbers below one hundred: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.

Two consecutive prime numbers are called twin primes if their difference is equal to two. If you have a look at the list of prime numbers above, you will realize that the first pairs of twin primes are (3, 5), (5, 7), (11, 13), (17, 19), (29, 31), (41, 43), (59, 61), and (71, 73).

Since the great Euclid, §11, (around 300 BC) we know that there are infinitely many prime numbers. But, are there infinitely many twin primes?

Mathematicians believe that the answer is yes, but nobody has been able to prove this conjecture yet.

Note that the only even prime is 2, so twin primes are as closely spaced as possible for two primes -with a gap distance of 2-, except for the pair (2, 3) with a gap distance of 1. In April 2013, Yitang Zhang announced the discovery that there are infinitely many pairs of primes that differ by a gap of some number below approximately 70,000,000. Two years later, in 2015, James Maynard and his group showed that there are infinitely many pairs of primes that differ by at most 246. This number is quite closer to the number 2 of the twin primes conjecture than the first result involving the number 70,000,000. The conjecture about twin primes is likely to become a theorem soon! (We hope). Nowadays, the math community is trying to reduce this large gap of 246 to just 2 units.

34. Archimedes: The first giant of mathematics

Archimedes was born in Syracuse (ancient Greece) in 287 B.C. He was a great scientist with brilliant contributions to physics, astronomy, and maths. He discovered the concept of density and formulated the principle of buoyancy, which explains why some objects float but some others sink. He stated the laws of the lever and pulleys.

He was also a great inventor. He invented the so-called Archimedean screw, other machines to be used in astronomy observations and calculations, and many war machines that allowed defending his city against the Romans.

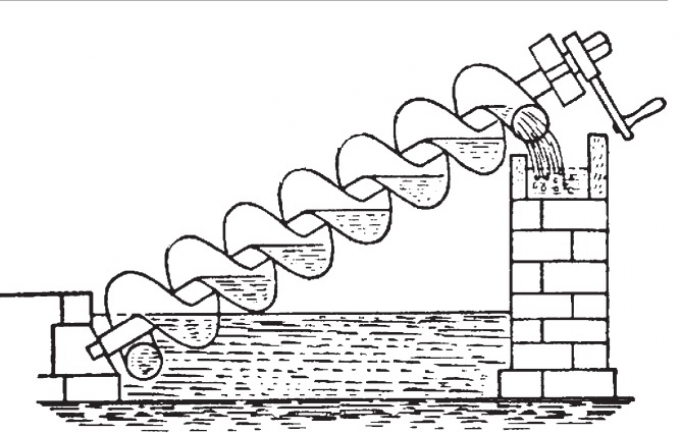
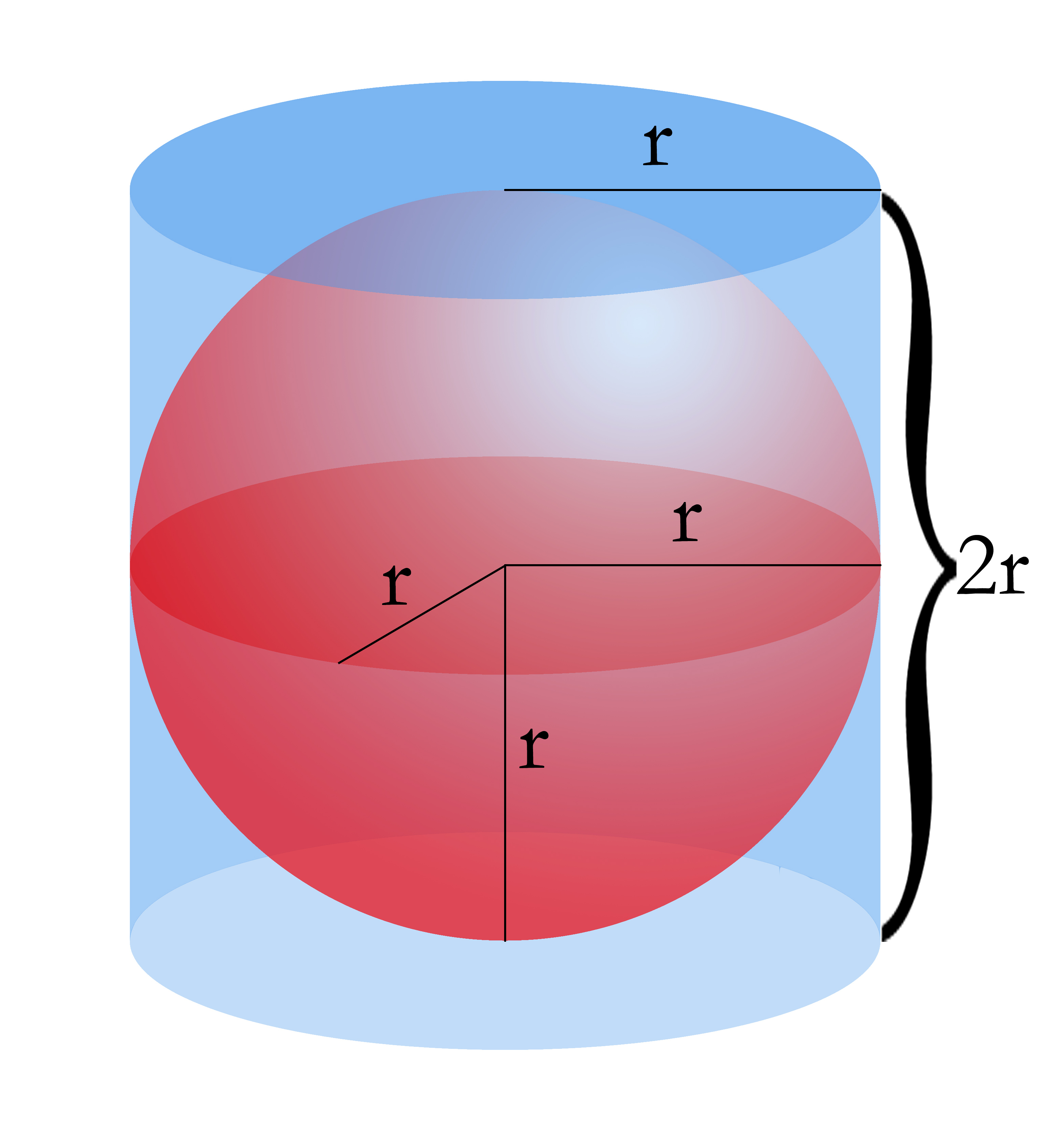
But above all, Archimedes was a giant mathematician. He estimated the value of the number ?=3.14... starting with the perimeters of inscribed and circumscribed regular polygons. He also made important discoveries about the volume and the surface of spheres and cylinders.

He was a clear example of an absent-minded mathematician. One time, Archimedes was working on a problem he had drawn on the sand of the floor. His city, Syracuse, was in war against the Romans, and it had been taken just when he was thinking about the problem. Then a Roman soldier showed up and shouted at him:

"I order you to come with me to see the General"

But Archimedes answered impatiently:

"Can't you see I am working? I must finish my problem firstly. And stand off my diagram, you are spoiling it"

The soldier got angry, drew his sword and killed Archimedes.

35. I love polydivisible numbers

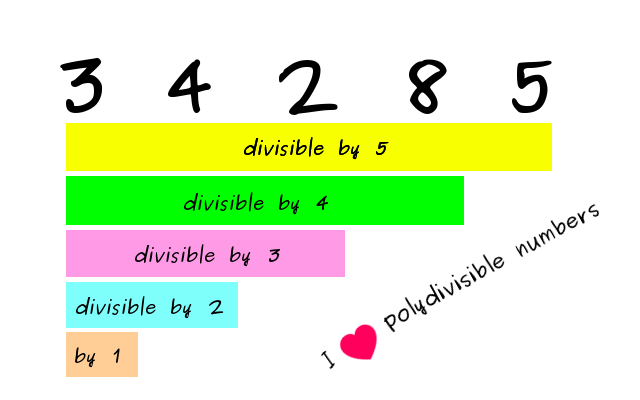
Is it possible to write a nine-digit number so that its first digit is divisible by 1, its two first digits are divisible by 2, its three first digits by 3, and so on until the whole nine-digit number is divisible by 9?

Let's try to build such a number starting from left to right, digit by digit. Any number from 1 to 9 will work to start with, as every integer is divisible by 1. Let's say number three:

3

The second digit must be even to ensure that the entire number is divisible by 2. Let's say 4. So, our number is now

34

Ok, do you remember the divisibility rule for 3? Sure, the sum of the digits has to be divisible by 3. The number

342

fulfills the rule (3+4+2=9), and so do the numbers 345 and 348. But let's continue with 342. I like that number.

The divisibility rule for 4? The last two digits have to be divisible by 4. The number

3428

is suitable, as 28 is divisible by 4 (so the entire number is divisible by 4, too). If we add the digit 0 or 5 to the right we would have a number divisible by 5. As we are not using the digit 0 (remember: only from 1 to 9), the only option is

34285

All right. The rule for 6? The number should be divisible by both 2 (so it must end in an even digit) and 3 (so their digits must add up to a multiple of three). The number

342852

will do (and also 342858, which is 6 units more... but I like the former more, for no reason).

We are on the right track. There are only three digits left! Let's add another one that makes the number divisible by 7... Well, I have to confess that I don't remember the divisibility rule for 7 (it's a bit tough) but I do know how to divide. So, let me try my luck with the number 3428529 (I have put 9 as a possible seventh digit). I take my pencil, divide 3428529 by 7 and' bad luck, the division is not exact: It gives a remainder of 6. But that's the clue' if we subtract 6 units to the failed candidate 3428529, we get for certain a number divisible by 7:

3428523

Ugh... we are almost done. With the same trick applied to number 8 we can get the next digit and then write

34285232

Finally, a number is divisible by 9 if its digits add up to a number that is divisible by 9 (yeah, I do remember the rule for 9!). I'm going to add... 3+4+2+8+5+2+3+2=29... so we must add 7 as the final digit to allow the sum to be 36, which is a multiple of 9. Perfect, we are done! Our number is:

342852327

Wow, we did it!

Can you make other numbers with the same property? Sure you can as there are many more choices (concretely 2,492 altogether). These numbers are called polydivisible numbers.

But don't relax, yet... You know that mathematicians like to impose additional conditions in order to complicate things. For example, if each number from 1 to 9 is allowed to appear exactly once, is it now possible to build a polydivisible number with the nine digits? The answer is yes, but this time there is a unique solution: 381654729 (see references on the web for a witty deduction' or try it by yourself)

And you also know that mathematicians love generalizing. So, we can consider polydivisible numbers with more than 9 digits. For instance, 10200056405 is a 12-digit polydivisible number (you can check it). Obviously numbers from 0 to 9 can be repeated. With many digits involved getting a polydivisible number becomes more and more difficult. Then, the burning question is: Are there infinitely many polydivisible numbers? And the answer is' nope. There are only 20,456 polydivisible numbers altogether, with

3 608 528 850 368 400 786 036 725

being the longest one. In fact, this is the only 25-digit number that is polydivisible. The next graph shows the number of polydivisible numbers in terms of the number of digits' read the last sentence again and more slowly if needed ;-)

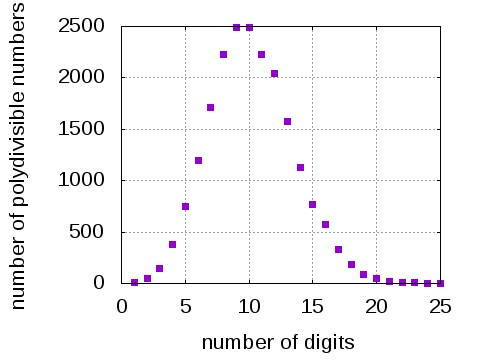
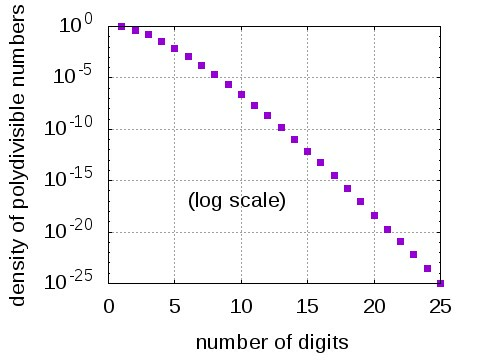
The density of n-digit polydivisibility numbers can be defined as the ratio between the number of polydivisible numbers with n digits and the total numbers with n digits (i.e. 10ⁿ). For 1-digit numbers the density is 1 (all numbers are polydivisible), while for 26-or-more-digit numbers the density is strictly zero (none is polydivisible). Have a look at the graph below.

36. Euler: A prolific mathematician

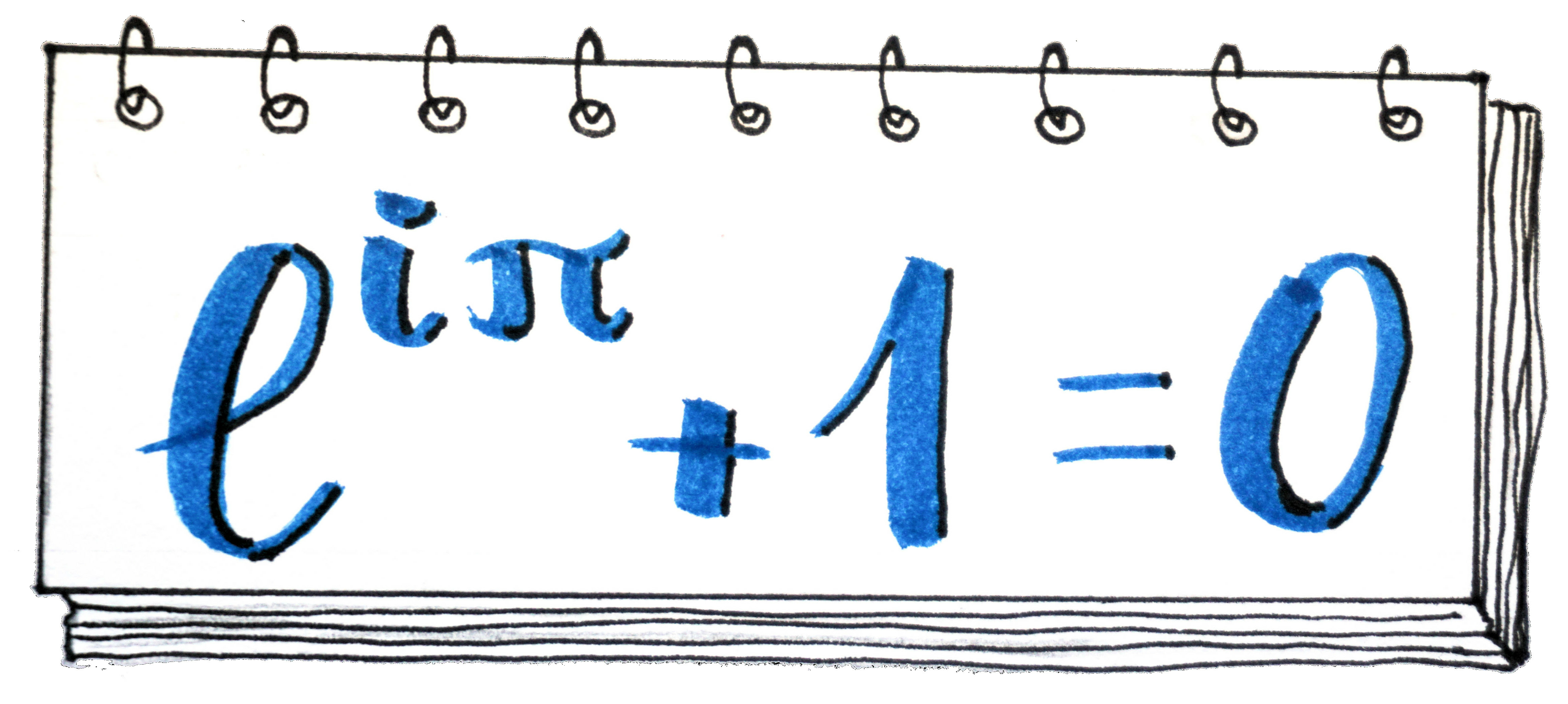
Leonhard Euler was born in Switzerland in 1707. He is considered the most prolific mathematician in history (based on the number of pages, while Paul Erdös, §5, published more articles). It is said that he could write a mathematical paper in the half-hour between the first and second call to dinner!

As soon as Euler finished a paper, he would put it on top of a growing pile that was awaiting for being printed. Then, the printer would grab the articles from the top and therefore many times the dates of the publication of Euler's papers ran counterwise to those of their composition. It was extremely misleading because some papers, which were based on previous ones, were actually published first.

In the first picture you can see Euler's identity, one of the most beautiful formulas in mathematics. It combines the important numbers e=2.71828..., ?=3.14159..., i=?-1, 1 and 0.

The second picture is a stamp containing another famous formula by Euler: for any convex polyhedron, the number of vertices and faces together minus the number of edges equals 2.

37. Hailstone Numbers

Hailstone numbers are the numbers of a sequence which is obtained as follows. First, start with any number. Then,

• if the number is even: divide by 2
• if the number is odd: multiply by 3 and add 1

Using the new number apply the previous condition again. Here we illustrate this algorithm, starting with the number 10:

10, 5, 16, 8, 4, 2, 1, 4, 2, 1'

We can see that this sequence loops into an infinitely repeating 4,2,1 sequence.

If we tray any other number, say 58:

58, 29, 88, 44, 22, 11, 34, 17, 52, 26, 13, 40, 20, 10, 5, 16, 8, 4, 2, 1, 4, 2, 1'

we see the same loop of 4, 2, 1.

Hailstone numbers are called like that because they typically rise and fall, resembling a hailstone inside a cloud. Every tested starting natural number has produced a hailstone sequence that eventually drops down to the number 1, then "rebounding" into the loop 4, 2, 1.... You can imagine that it is a hailstone heavy enough to fall from the cloud to the ground and then bounce.

The proper mathematical name for this investigation is the Collatz conjecture which was made in 1937 by the German mathematian Lothar Collatz.

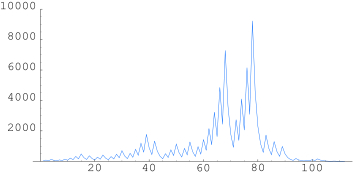
The following graphic shows how different numbers (x axis) take a different number of iterations (y axis) to reach 1. We can see that some numbers take much longer than others to reach one.

38. The returning explorer revisited

The brilliant Martin Gardner reviews the old riddle of an explorer who walks one mile due south, turns and walks one mile due east, and finally turns again and walks another one mile due north, arriving at exactly the same point where he started. How is this possible?

This problem is known as the returning explorer, and sometimes it is said that the explorer shoots a bear after his walk. Then you are asked to figure out the color of the bear. After thinking for a while, smart people answer "white", as the explorer must have been in the North Pole of the Earth (the blue point in figure below) when shooting the (polar) bear. This would explain his closed trajectory (red spherical triangle in the figure below). The graph is not to scale.

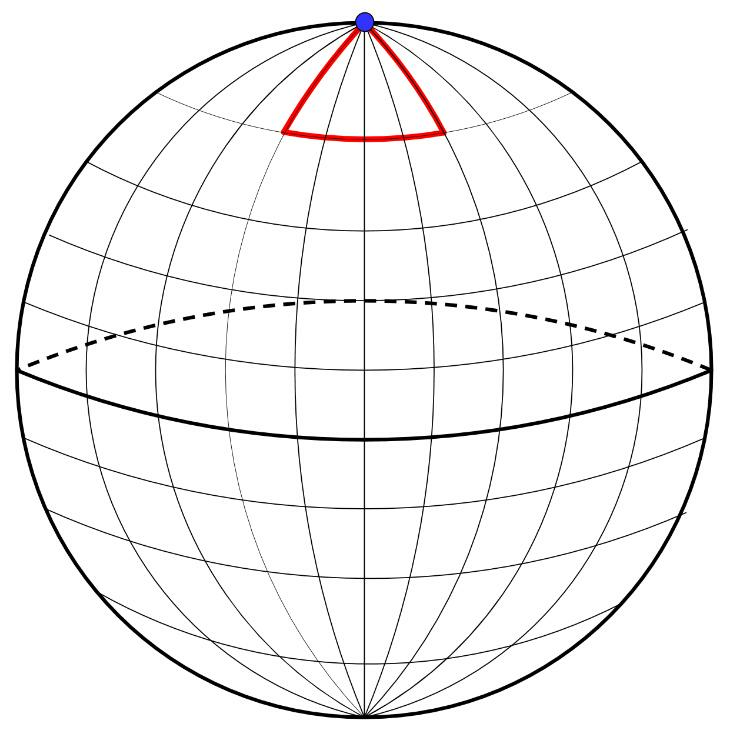
A mathematician would only partially agree with the answer above and would ask more questions. Is this the only spot on Earth for the returning explorer? Can you find other points, besides the North Pole, from which the explorer could walk a mile south, a mile east, a mile north and then find himself back at his starting position?

The answer is definitely yes. In fact, there are infinitely many points. Let me explain it. Imagine a parallel line on the Globe so close to the South pole that its total length is precisely one mile: If you walk one mile East along this one-mile parallel, you will return to your original place. Therefore, if the explorer is in any point over another parallel located one mile north to the one-mile parallel, it would be a "returning explorer" after going south, east -honestly a waste of time- and north back to his starting position.

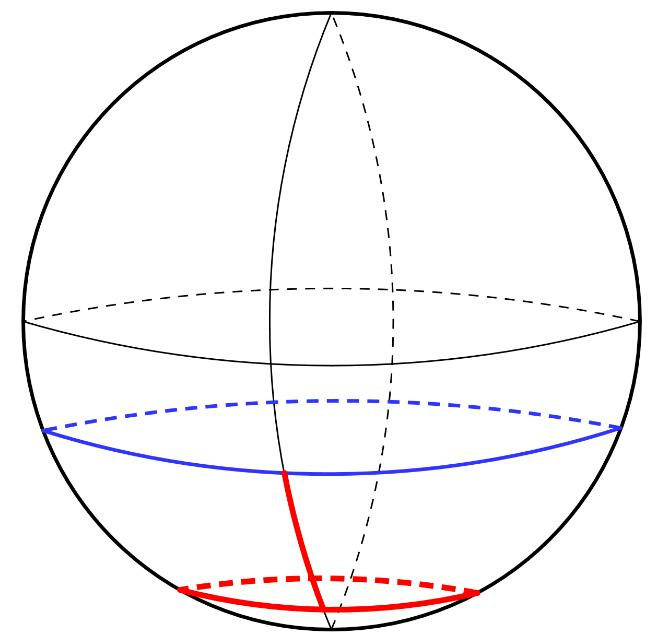
The infinitely many points that ensure a closed trajectory (in red for one of the points) are colored blue in the above figure. (The draw is not to scale.)

Moreover, the same idea applies to a half-mile parallel, a third-mile parallel and so on, with the only difference that the explorer would do 2, 3, etc. full turns in his Eastward trajectory.

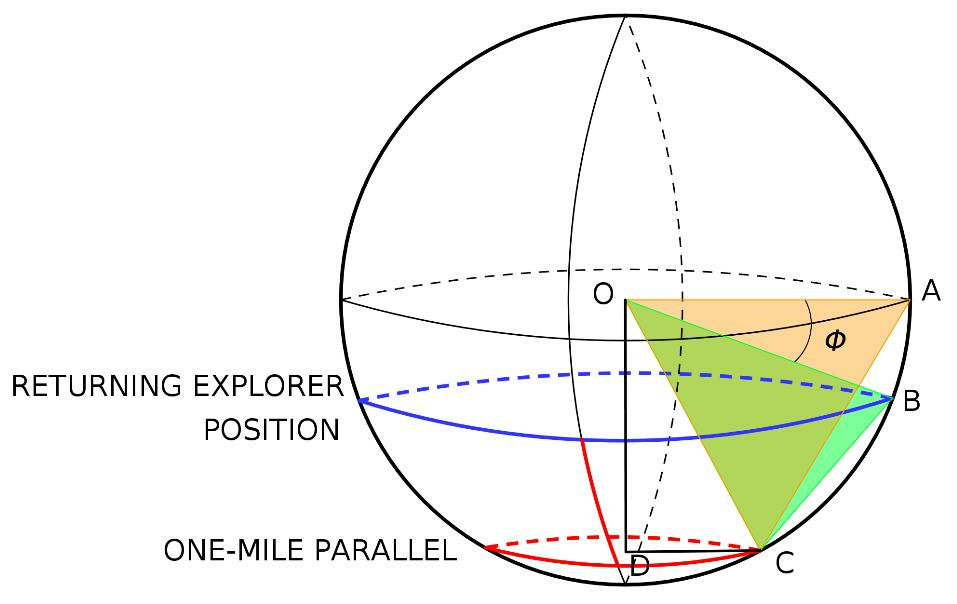
Let us calculate the latitude of the blue parallel that ensures going back to the starting point (see the previous figure). The length of the red parallel is 1 mile, and the length of a circumference is given by the formula 2?r, thus

2?r = 1,

which gives us the radius r between D and C (see figure):

r = 1/(2?)

Now, remember that the cosine of the angle OCD (let us call it ?') is the quotient between DC (that is r) and OC (that is the radius of Earth R):

cos(?') = r/R

Combining the last two expressions and solving for ?' with the inverse function of the cosine (that is called arccos), we obtain

?' = arccos(1/(2?R))

Note that this angle ?'=OCD is equal to the angle AÔC, and therefore it represents the latitude of the one-mile parallel (red line in the figure).

Now let us compute the angle ?? between the red parallel and the blue one (see green triangle in the graph). The blue parallel is where the returning explorer is actually located. From the definition of a radian (the standard unit of angle measure) we can calculate this angle as the quotient of the arc length for BC -which is 1 mile- and the radius of Earth R:

?? = 1/R

Finally, the latitude of the blue parallel is ?=?'-??:

? = arccos(1/(2?R)) - 1/R

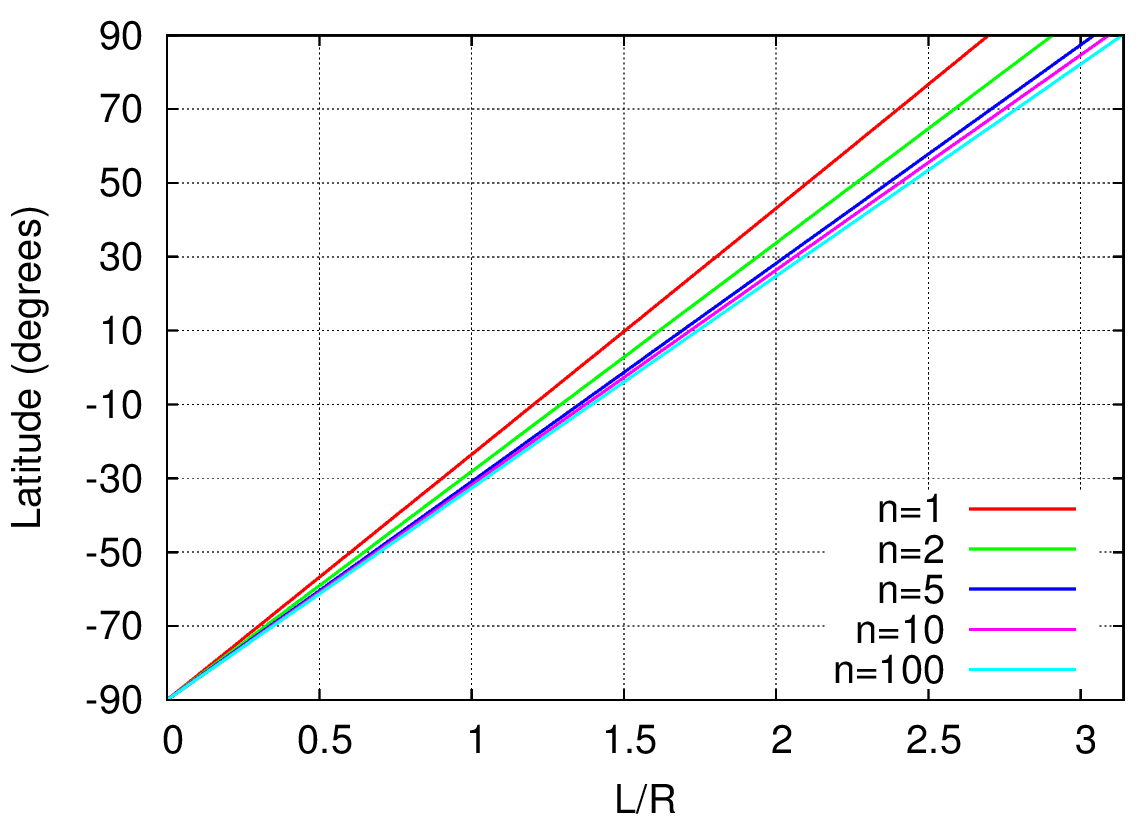
This angle is expressed in radians, but normally latitude is expressed in degrees (0 degrees for the Earth's equatorial plane, 90° for the North Pole, and -90° for the South Pole). Thus, we must multiply by the factor of conversion 180/? and change the global sign to get negative latitudes for the Southern Hemisphere. Moreover, it is straightforward to generalize the previous formula to include trajectories along red parallels of a 1/n of a mile, with n being the number of full turns (n = 1, 2, 3,...). We can also consider that the explorer walks an arbitrary distance L in each direction instead of just 1 mile. Then, the general formula for the latitude in the South of the returning explorer would read:

? = 180/?·[L/R - arccos(L/(2?nR))] (Latitude, degrees)

This formula is only valid for values of L that result in an angle ? between -90° and 90°. There always are solutions for some n providing that L < ?R (although for n=1, L should be less than approximately 2.7R). In the next graph, the latitudes in terms of the quotient L/R are shown for some values of n.

The length of the arc between the South Pole and a point along one of the infinitely many blue parallels (one for each valid value of the natural number n) is the product of its subtended angle in radians, ?/2 + ?, and the radius R, which gives:

Arc = L + R·[?/2 - arccos(L/(2?nR))] (distance from the South Pole)

The previous two general exact expressions can be approximated for small values of L/R, as in the original example, where L=1 mile and the average Earth's radius R is over 3960 miles. To the first order at L/R, they read:

? ? -90 + 180L/(?R)·[1+1/(2?n)]
Arc ? L·[1+1/(2?n)]

The last expression for L=1 mile and n=1 is the one that Martin Gardner tell us, and it gives a distance of approximately 1.16 miles from the South Pole. For greater values of n, the parallels are even closer to the South Pole.

In any case, there are no bears in Antarctica, so these infinitely many points near the South Pole that ensure a returning trip for the explorer are not valid and we must admit "white" as the perfect answer for the color of the bear. But it wasn't that obvious at all, was it? Now, we know that the explorer could also be shooting black and white penguins (with a camera).