Manuel Feito Guzmán

Las Otras Matemáticas
(Textos para todos los públicos)

Textos en Castellano

En esta sección se presentan 25 textos en castellano que contienen multitud de anécdotas, historias, curiosidades y aplicaciones de las matemáticas.

1. Adiós intuición, hola matemática

Cuando la intuición falla, las matemáticas vienen a echarnos un cable. Y de eso vamos a hablar: de cables. Imaginad uno larguísimo que diera la vuelta al planeta, pongamos por el ecuador, de manera que los dos extremos se tocaran a malas penas, o sea, sin que sobrara nada. Imaginad ahora que separamos el cable un solo centímetro de la superficie de la Tierra a lo largo de toda su extensión. Entonces el cable se va a quedar corto y los extremos ya no llegarán a tocarse. Falta cable, eso está claro, pero cuánto. Así a ojo, habiendo separado solo 1 centímetro el cable, ¿cuánto diríais, más o menos, que nos faltaría para volver a unir los extremos?

¿Ya? ¿Habéis hecho una apuesta? Pues ahora vamos a las cuentas. Adiós intuición, hola matemática.

Veamos, el cable alrededor del ecuador forma una circunferencia cuya longitud, que denotaremos por la letra ? minúscula, viene dada por la fórmula

? = 2?r, (1)

donde ? es el número pi (del que ya hablamos más en §16 y en §18) y r es el radio de la Tierra. El (1) entre paréntesis es para nombrar esta primera ecuación que luego vamos a usar.

Si separamos el cable de la Tierra ahora tendremos un radio mayor, que podemos llamar R mayúscula, y la nueva circunferencia tendrá por longitud

L = 2?R. (2)

Como R es un centímetro mayor que r podemos escribir

R = r + 1, (3)

con lo que la ecuación (2) quedaría como L = 2?(r+1). O bien, usando la propiedad distributiva para quitar el paréntesis:

L = 2?r + 2?. (4)

Y como 2?r es precisamente la longitud del cable pegado a la Tierra, como vimos en la ecuación (1), entonces podemos escribir la ecuación (4) como:

L=?+2? (5)

¿Y qué nos dice esta ecuación última? Pues que la longitud del cable separado, L mayúscula, solo se diferencia de la longitud del cable pegado, ? minúscula, en 2?. Como ? vale aproximadamente 3,14, la diferencia es aproximadamente de 6,28. Y como diría la profesora de física y química, ¿6,28 qué?, ¿peras, manzanas, euros? Pues está claro, en la ecuación (3) el 1 era en realidad 1 centímetro, así que ahora este 6,28 son 6,28 centímetros.

¡Ajá! ¡Menos de 7 cm de diferencia! ¿Funcionó vuestra intuición? ¿Sí?, bien. ¿No?, ¿pensabais que 1 solo centímetro a lo largo de los miles de kilómetros del ecuador se iba a ir acumulando y que nos faltaría un montón de cable al final?

Pero las ecuaciones dicen todavía más cosas. Si os fijáis con cariño en la ecuación (5) veréis que el resultado no depende del radio. De hecho, tampoco hemos usado en ningún momento el valor del radio de la Tierra. Así que esos 6,28 centímetros serían también la longitud que nos faltaría si primero ajustamos el cable alrededor de una moneda y luego lo separamos 1 cm por todos lados. Da igual el tamaño de la circunferencia.

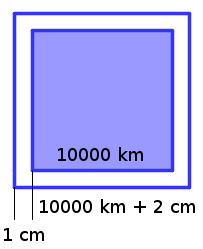
Por si todavía queda algún escéptico que confía más en su intuición errónea que en las matemáticas, os pongo todavía un ejemplo más claro, con números, para que no haya que marearse con fórmulas. Y para que sea más fácil, en vez de un planeta esférico vamos a imaginarnos un planeta plano y cuadrado. Pongamos que tiene 10.000 kilómetros en cada lado y que le colocamos el cable alrededor, o sea, que gastamos 40.000 km de cable. Ahora separamos el cable 1 centímetro por todos los lados, ¿cuánto cable necesitaríamos? Pues los 40.000 km de antes y 8 centímetros más como podéis ver en la imagen de abajo. Es verdad que esta vez no salen los 6,28 centímetros de las circunferencias, pero 8 centímetros es bastante parecido. Desde luego no son kilómetros y kilómetros de cable extra.

Y si todo esto no ha humillado aún vuestra intuición, esperad a leer §4 y §30.

2. Halley: un cometa de un hombre perseverante

Edmond Halley (1656-1742) fue un matemático, físico y astrónomo inglés que pasó a la historia por ser el primero en determinar el periodo de un cometa, es decir, cada cuántos años pasa cerca de la Tierra y, por lo tanto, podemos observarlo en el cielo a simple vista.

A ese cometa se le conoce, en su honor, como "cometa Halley". Su periodo es de unos 75 años y la última vez que pudimos observarlo fue en 1986. Así que tendremos que esperar hasta 2061 para volver a verlo por aquí cerca.

Edmond Halley fue un científico generoso y perseverante. Gracias a su insistencia y a su apoyo económico se publicaron los famosísimos Principia de Isaac Newton: uno de los libros científicos más relevantes de la historia.

Pero lo siguiente sí que es una muestra de perseverancia. En aquellos años, se acababa de encontrar una copia en árabe de un trabajo del físico y matemático griego Apolonio. El astrónomo Edward Bernard, gran conocedor del árabe, empezó a traducir la copia de Apolonio, pero murió cuando llevaba solo 13 páginas. Halley se propuso seguir la traducción. Eso sí, Halley no tenía ni idea de árabe. Pero lo tradujo. ¿Cómo? Estudió con detalle las 13 páginas de la traducción que ya estaba hecha y comenzó, poco a poco, a reconocer palabras por el contexto. Luego fue sacando el significado de palabras nuevas por la argumentación y así, con esfuerzo y perseverancia, completó la traducción.

3. Pero... ¿qué es eso de una proposición?

En matemáticas, una proposición es una afirmación que puede ser demostrada lógicamente partiendo de axiomas, postulados o de otros resultados que previamente han sido también demostrados. Es decir, una proposición es lo mismo que un teorema matemático, solo que algo menos importante (se suele reservar el nombre de "teorema" para los grandes resultados).

Puesto que las proposiciones -y sus hermanos mayores los teoremas- pueden ser demostrados, eso nos asegura su validez inmutable. Son verdades eternas. El teorema de Pitágoras es y será siempre cierto. Y esto es algo muy particular de las matemáticas, que las distingue de las ciencias experimentales. Porque en física, por ejemplo, las cosas son como son..., pero a veces llega alguien y encuentra una teoría más exacta y echa por tierra todo lo anterior. Con el teorema de Pitágoras eso no puede ocurrir. Está ahí ya para siempre.

Así que el punto clave de toda proposición es que sea matemáticamente cierta, o sea, verdad de la buena. Y para ello no queda más remedio que demostrarla con argumentos irrefutables. Vamos a ver un ejemplo con una proposición que no encontraréis en ningún libro, porque es tan tonta que probablemente no tiene ningún interés. Esta es la proposición:

Entre el número 10 y el número 20, ambos inclusive, hay más números compuestos que primos.

Tenéis que recordar que los números primos son aquellos números naturales mayores que 1 que solo se pueden dividir de forma exacta entre ellos mismos y entre el número 1. Los primeros números primos son 2, 3, 5, 7, 11... Por contra los compuestos son los números mayores que 1 que sí que tienen más divisores. Los primeros números compuestos son 4, 6, 8, 9, 10...

Bien, pues vamos a demostrar la proposición... y lo vamos a hacer de dos formas distintas, que no se diga.

Demostración 1:

El 10 es compuesto (aparte de por 10 y por 1, puede dividirse entre 2 y también entre 5). Y podemos ir haciendo lo mismo hasta el 20 para ver si el resto de números son primos o compuestos. Con la descomposición factorial se ve muy claro:

10=2·5 (compuesto); 11 primo; 12=2²·3 (compuesto); 13 primo; 14=2·7 (compuesto); 15=3·5 (compuesto); 16=2⁴ (compuesto); 17 primo; 18=2·3² (compuesto); 19 primo; 20=2²·5 (compuesto).

La conclusión de lo anterior es que entre 10 y 20 hay más números compuestos (10, 12, 14, 15, 16, 18, 20) que primos (11, 13, 17, 19), que es lo que queríamos demostrar.

Demostración 2:

. Como los números pares y los impares se van siempre alternando, resulta que en el conjunto de números entre el 10 y el 20, ambos inclusive, hay más pares que impares (puesto que tanto el 10 como el 20 son pares).

. Todos los números pares son compuestos (salvo el 2, que no está en nuestro conjunto) ya que pueden dividirse de manera exacta entre 2 (y no solo entre ellos mismos y entre 1, que era el requisito para que fueran primos).

Uniendo las dos afirmaciones anteriores se deduce inmediatamente lo que queríamos demostrar: hay más números compuestos que primos en el intervalo entre 10 y 20 porque hay más pares y acabamos de ver que esos pares son compuestos.

Pues ahí están las dos demostraciones. Ambas son perfectamente válidas pero parece claro que la segunda es más elegante. Y no solo eso, sino que tiene ventajas innegables. En primer lugar, es más rápida, puesto que no hay que ir probando uno a uno los números. De hecho, la demostración 2 no involucra ninguna operación. Y en segundo lugar, la demostración 2 puede generalizarse a otros casos: por ejemplo, siguiendo el mismo razonamiento podemos demostrar esta otra proposición:

Entre el 1802 y el 1818, ambos incluidos, hay más compuestos que primos.

O incluso esta otra más general:

En el conjunto de números comprendidos entre n y m, ambos incluidos, siendo n y m números pares (distintos de 2), hay más números compuestos que primos.

¿Veis por qué hay que decir que n tiene que ser distinto de 2?

Así que definitivamente nos quedamos con la segunda demostración, que es más elegante y mejor que la primera demostración por "fuerza bruta". Sin embargo, hay veces que para algunas proposiciones los matemáticos no encuentran una demostración "directa" como la segunda y se se ven abocados a usar un método exhaustivo como el primero. Quizá el caso más famoso de demostración por fuerza bruta sea el del Teorema de los cuatro colores, §6. Y por cierto, hay más formas de demostrar las cosas, como por ejemplo el método de "reducción al absurdo" que tan genialmente utilizó Euclides para demostrar la infinitud de los números primos, §11.

4. El sorprendente caso del problema del cumpleaños

Una clase de tamaño normal en un instituto de secundaria, digamos de 30 alumnos. Un profesor de matemáticas alegre que propone al principio de curso hacer una pequeña celebración el día del cumpleaños de cada uno. O sea, 30 fiestas... ¡Espera! A lo mejor son menos fiestas de cumpleaños, porque puede darse la casualidad de que dos alumnos de la clase cumplan años el mismo día. No hay gemelos en la clase, así que eso parece mucha casualidad... ¿o no tanta?

Pues vamos a calcular cuál es esa probabilidad de forma exacta. Pero antes hay que repasar algunas cosas:

. Aunque normalmente decimos que la probabilidad de que llueva es del 75%, los matemáticos nunca dan la probabilidad en tanto por ciento, sino en "tanto por uno". Diríamos entonces que la probabilidad es 0,75. Así que algo que ocurra seguro (100%) tiene una probabilidad de 1.

. Si la probabilidad de que llueva es del 75% (perdón, hemos dicho que se dice en tanto por uno: 0,75), entonces la probabilidad de que no llueva es del 25% (perdón de nuevo: 0,25). Así que la probabilidad de una cosa se puede obtener calculando la de lo contrario y restándosela al número 1.

. Si lanzamos un dado y nos preguntamos por la probabilidad de que salga un número par, la probabilidad será 3/6 = 0,5 porque hay 3 casos favorables que nos valen (los números pares: 2, 4 o 6) de 6 casos posibles (1, 2, 3, 4, 5 o 6). Esto funciona siempre que el dado no esté trucado (en general, se dice que los sucesos elementales han de ser equiprobables) y se llama regla de Laplace (la volveremos a usar en §18 para calcular el número ? a cañonazos):

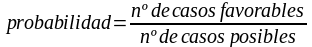
. Si en vez de 1 dado tiramos 3 dados y queremos que salga un número par en los tres a la vez, entonces la probabilidad de que eso ocurra se obtiene multiplicando las probabilidades de cada uno de ellos por separado, lo que da 0,5·0,5·0,5=0,125. Esta regla de multiplicar las probabilidades funciona siempre que los "experimentos" individuales sean independientes uno de otro.

Volvamos a nuestra clase de 30 alumnos. Queríamos saber la probabilidad de que hubiese al menos dos personas que cumplieran años el mismo día. Vamos a hallar primero lo contrario, es decir, la probabilidad de que nadie cumpla años el mismo día, y luego se la restamos a 1.

Podríamos hacerlo de la siguiente forma. El primer alumno dice su fecha. El segundo alumno habla a continuación. Lo normal es que no cumpla años el mismo día que el primero. De hecho, le valen para no coincidir 364 días de los 365 días del año. Así que, de acuerdo a la regla de Laplace, la probabilidad de no coincidir para el segundo alumno será 364/365. Y ya hay dos fechas cogidas. El tercer alumno tiene entonces 363 días favorables de los 365 días posibles del año: una probabilidad de 363/365. Y cuando llegamos al último alumno, ya habría 29 fechas cogidas y quedarían libres, por tanto, 336, con lo que su probabilidad de no coincidir es de 336/365.

Pues ahora ya está casi. La probabilidad de que cada uno de ellos tenga una fecha única la podemos obtener multiplicando las probabilidades anteriores, es decir,

364/365 · 363/365 · ··· · 336/365

El resultado que da esta cuenta es 0,294. Eso, en porcentaje, es un 29,4%. Y la probabilidad de lo contrario, a saber, de que SÍ haya gente en la clase que cumpla años ese mismo día, es del 70,6%.

Así que hay casi un 71% de que SÍ haya coincidencias frente a un 29% de que NO. El resultado puede parecernos sorprendente y por ello que incluso se conoce este problema como la paradoja del cumpleaños. De hecho, haciendo el mismo razonamiento, puede verse que, a partir de solo 23 alumnos en la clase, es más probable que dos o más celebren el cumpleaños el mismo día a que no lo hagan. Y a partir de grupos de 41 personas la probabilidad se eleva ya a más del 90%.

Por último, habría que señalar algunos detalles si queremos profundizar un poco:

. No hemos tenido en cuenta que los años pueden ser bisiestos. Pero considerar que a veces los años son de 366 días en lugar de 365 no aporta mucho cambio.

. Cuando se trata de nacimientos, las fechas en que ocurren no son equiprobables. Aunque no hay mucha diferencia, en algunos meses del año la natalidad es superior. Stricto sensu no podríamos haber aplicado la regla de Laplace por aquello de que los sucesos tenían que ser equiprobables. Pero en cualquier caso la aproximación es bastante acertada e incluso tener en cuenta estas sutilezas haría que todavía fuese más probable la coincidencia.

. En realidad, si pensamos que es relativamente frecuente que haya gemelos en una misma clase, las probabilidades de coincidencias serían todavía mayores.

. No es difícil escribir la fórmula que nos da la probabilidad de coincidencia para una clase de n alumnos. Para n mayor o igual que 366 seguro que ya hay coincidencia (sin tener en cuenta años bisiestos) y la probabilidad sería 1. Para valores de n comprendidos entre 1 y 365 la fórmula es:

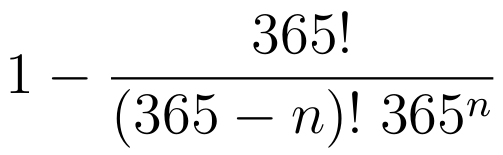
donde el signo de exclamación es el factorial (por ejemplo, el factorial de 6 es 6! = 720 porque 6·5·4·3·2·1=720).

. La fórmula anterior queda muy bien, pero no es demasiado práctica porque el factorial de 365 es un número tan gigantesco que no cabe ni en la calculadora. Por suerte, se compensa en parte con el factorial del denominador para valores bajos de n (es lo que nos pasó en nuestro ejemplo con n = 30). Para valores altos de n la cosa se complica y conviene usar aproximaciones a la función factorial.

En fin, de vuelta a nuestra clase resulta que probablemente el alegre profesor de matemáticas se perderá alguna fiesta de cumpleaños porque habrá que juntar dos el mismo día. O incluso a lo mejor cumplen años los 30 alumnos a la vez y hay una única fiesta antológica... aunque eso ya parece muy muy muy improbable... ¿o no tanto?, ¿qué pensáis?, ¿sabríais calcular esa probabilidad? Porque, después de lo que acabamos de contar y de lo de la cuerda alrededor del mundo que vimos en §1, parece que ya no puede uno fiarse mucho de su intuición.

5. Paul Erdös y su número

Paul Erdös fue un matemático húngaro del siglo XX. Se le considera, junto a Leonhard Euler, el matemático más prolífico de todos los tiempos, es decir, el que más trabajos matemáticos ha realizado (más de 1500 publicaciones).

Las posesiones materiales no significaban nada para Erdös, que solía donar los premios que recibía o los reinvertía como nuevos premios por la solución de problemas que él mismo proponía. Pasó la mayor parte de su vida viajando entre conferencias científicas y casas de colegas matemáticos alrededor del mundo. No tenía hogar.

Erdös colaboró con más de 500 matemáticos hasta su muerte en 1996. Se dice que un matemático tiene NÚMERO DE ERDÖS igual a 1 si ha firmado un artículo junto a Paul Erdös. Un matemático tiene número de Erdös 2 si ha hecho un artículo junto a un matemático que trabajó directamente con Erdös y así sucesivamente.

En 2004, un investigador con un número de Erdös 4 subastó en eBay la posibilidad de colaboración para obtener un número de Erdös de 5. La oferta final fue de unos 1000 euros.

Por cierto, el autor de este trabajo tiene también un honroso número de Erdös 4, puesto que es coautor con Hugo Touchette (Erdös 3), quien es coautor con Thomas Prellberg (Erdös 2), el cual es coautor con Peter J. Cameron (Erdös 1), coautor, a su vez, con Paul Erdös.

Y claro, el propio Erdös es el único que tiene número de Erdös 0.

6. Un mundo en cuatricromía: el teorema de los cuatro colores

¿Cuántos colores hacen falta para colorear un mapa sin que dos países o regiones adyacentes tengan el mismo color? ¡Cuatro nada más! ¿Seguro? Pues sí, segurísimo porque hay un teorema matemático para ello. El teorema de los cuatro colores fue conjeturado en 1852, pero la demostración no llegó hasta mucho mucho más tarde: un siglo y cuarto después. Y además, vino cargada de polémica...

Antes de nada, veamos qué dice el teorema de los cuatro colores. En lenguaje sin demasiados tecnicismos es algo así:

Cualquier mapa geográfico con regiones continuas se puede colorear con cuatro colores diferentes de forma que no queden países fronterizos con el mismo color.

Hay que tener en cuenta algunos aspectos básicos:

. Los países pueden modelizarse mediante lo que los matemáticos llaman grafos. Así que realmente el teorema de los cuatro colores puede formalizarse en un lenguaje mucho más complicado..., pero, vamos, al final, viene a decir lo mismo.

. Cuando se dice "cualquier mapa", se refiere efectivamente a cualquiera, bien sea un mapa real, o bien un mapa imaginario rarísimo que se nos ocurra dibujar.

. Los países han de ser "continuos" (los matemáticos dirían "simplemente conexos"), lo que quiere decir que no deben estar formados por regiones geográficas separadas (como ocurre, por ejemplo, con Alaska y el resto de EEUU), pues de lo contrario podría darse el caso de que dos partes de un mismo país no pudieran pintarse con el mismo color. De todas formas el mapa del mundo actual es tan simple (desde un punto de vista de grafos matemáticos) que, aunque haya algunas regiones aisladas del resto de su país, aun así es suficiente con cuatro colores para asegurar que todas las partes de un mismo país son del mismo color.

. El agua no se colorea, se deja en blanco. En caso contrario necesitaríamos, en general, un color más.

. Los países pueden tener un punto en común del mismo color, pero no una línea. Es lo que ocurre en el siguiente mapa imaginario con 6 países con forma triangular y que con solo 2 colores pueden distinguirse claramente.

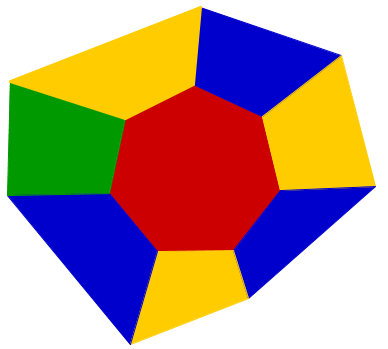
Como en el ejemplo anterior, hay casos en los que necesitamos menos de cuatro colores. Lo que el teorema dice es que con cuatro colores seguro que tenemos suficiente para cualquier mapa continuo. Nunca jamás vamos a necesitar un quinto color si elegimos con buen criterio el color para cada país... ¿Y es muy difícil pensar en un mapa en donde necesitemos usar todos los colores, o sea, los cuatro? Pues no, es lo que ocurre cuando tenemos un país con un número impar de vecinos con frontera entre sí:

Pero claro, un teorema necesita una demostración para dejar de ser una mera conjetura, §3. Y, como dijimos al principio, esa demostración costó mucho tiempo. Desde que Francis Guthrie conjeturó en 1852 que cuatro colores eran suficientes, se sucedieron bastantes supuestas demostraciones que resultaron ser erróneas a la postre. Hasta que en 1976, K. Appel y W. Haken consiguieron reducir el problema a algo menos de 1500 configuraciones. Aunque usaron conceptos complicados de teoría de grafos, eso quería decir, en el fondo, que era como si todos los mapas imaginables fueran, o bien casos que ya se sabía que necesitaban 4 o menos colores, o bien casos que pudieran clasificarse en uno de los 1500 mapas reducidos que ellos propusieron. Con lo cual, solo hacía falta estudiar esos 1500 mapas...

Pero seguían siendo muchos mapas para colorear. Lo bueno es que ya no se trataba de probar con infinitos mapas imaginables, como al principio, sino que ahora había que "colorear" un número finito. Y 1500 mapas podían ser mucho para una persona, pero no para un ordenador con la potencia de cálculo de los que ya se estaban construyendo por aquella época. En concreto, el ordenador estuvo haciendo cálculos durante 1200 horas, o sea, ¡50 días completos! Y al final la conclusión fue la sospechada: todos los mapas podían ser coloreados con 4 colores o menos.

La demostración fue más que polémica. Primero, porque no era una prueba elegante como las demostraciones por reducción al absurdo clásicas, §11, o las contundentes demostraciones directas de toda la vida, §3. Era una demostración por fuerza bruta. Y segundo, porque los cálculos eran tantos que ni siquiera un humano podría reproducirlos en un tiempo razonable. Dependía directamente de una máquina. ¿Y si la máquina estaba mal programada? ¿Y si una operación fallaba porque un circuito sufría una subida de tensión?

Sea como fuere, la comunidad matemática acabó aceptando como válida la demostración. Y años después, en 1997 y en 2005, nuevas pruebas, también informáticas (¡ay!), corroboraron una vez más el teorema de los cuatro colores.

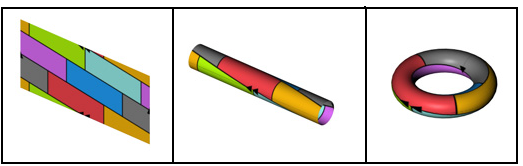
Antes dijimos que "nunca jamás" íbamos a necesitar un quinto color. Bueno, eso de nunca jamás suena demasiado definitivo ¿no? Lo cierto es que este es un resultado que vale para mapas en un plano bidimensional (como los ejemplos que mostramos aquí) o incluso para mapas curvos sobre una esfera (pensemos en una bola del Mundo con la esfera terrestre). Se dice que el número cromático de estas superficies es 4. Pero hay otras superficies más complejas. Por ejemplo, si encontráramos un planeta con forma de Donuts (esa forma se llama en matemáticas un toro) y tuviéramos que hacer un mapa con sus regiones (puestos a imaginar, pensemos que en ese planeta sus habitantes también tuvieran una organización en países y regiones como nosotros), entonces es posible que con 4 colores no tuviéramos suficiente, porque el número cromático de un toro es 7. Es decir, que, si en el Planeta Toro deciden hacer una división geográfica con mala idea, como la de la imagen de abajo, harían falta 7 colores para separar los países. Pero no más, ¡eh!

7. Ramanujan y la matrícula de un taxi

Ramanujan fue un genial matemático de principios del siglo XX. Nació en la India y allí apenas pudo estudiar porque no tenía libros. Sin casi formación matemática, era capaz de intuir fórmulas que permitían encontrar resultados interesantísimos, como la que se ve abajo, que permite en cada iteración de la serie infinita obtener 8 decimales más del número pi.

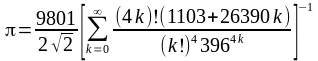
Ramanujan envió cartas mostrando sus "descubrimientos" a varios matemáticos importantes del Reino Unido, pero casi nadie les dio importancia..., excepto G. H. Hardy, que quedó impresionado por aquellas extrañas fórmulas que resultaban ser ciertas. Así que Hardy invitó a Ramanujan a trabajar con él en Reino Unido.

Allí, la salud del matemático indio, que siempre había sido delicada, empeoró. Cuentan que, estando Ramanujan ingresado en el hospital, recibió la visita de su amigo Hardy, que le dijo:

He venido en un taxi con el número 1729, un número nada interesante.

Y Ramanujan le respondió:

¡No! ¡Es un número muy interesante! Es el número entero positivo más pequeño que puede expresarse como la suma de dos cubos de dos formas distintas.

En efecto: una forma es 1³+12³=1729, y la otra es 9³+10³=1729. Pero... ¿cómo se dio cuenta de eso Ramanujan así de repente? Cosas de genios. Desde entonces, al número 1729 se le conoce como "taxicab number".

8. La hipótesis de Riemann

La hipótesis de Riemann es una conjetura formulada por Bernhard Riemann en 1859. Constituye uno de los Problemas del Milenio (de esos pendientes de resolver; incluso te dan un millón de dólares si logras encontrar la solución, §26). De hecho, entre los matemáticos es casi unánime la idea de que se trata de uno de los problemas más difíciles de abordar (por no decir el que más). Aun así, vamos a intentar explicar en qué consiste la conjetura de Riemann en las siguientes líneas.

Tiene que ver con las soluciones de una determinada ecuación. Pero hagamos antes un poco de memoria de algunos conceptos básicos.

Todos sabemos resolver ecuaciones sencillas, como, por ejemplo, la siguiente ecuación de segundo grado:

x²-5x+6=0.

Tiene dos soluciones: x=2 y x=3 (se pueden comprobar sustituyendo en la ecuación y viendo que se cumple la igualdad). Los matemáticos prefieren decir que 2 y 3 son los ceros de la función f(x)=x²-5x+6. En otras palabras, si escribimos la ecuación anterior como

f(x)=0

podemos afirmar que al sustituir x por 2 nos da 0, o lo que es igual, f(2)=0. Y lo mismo para f(3). Así que resolver una ecuación es encontrar los ceros de una determinada función.

Pues bien, la hipótesis de Riemann se refiere a los ceros de una función concreta, o, equivalentemente, a las soluciones de la ecuación:

?(s)=0,

donde ?(s) es la llamada función zeta de Riemann. Dicha función es bastante más complicada que la f(x) anterior y no vamos a definirla en detalle. Lo más significativo es que ?(s) es una función donde en vez de números reales aparecen números complejos (por eso normalmente utilizamos la letra s -o a veces z- en lugar de x). ¿Números complejos? Seguimos con el repaso.

Los números reales son los que estamos acostumbrados a manejar y que se representan en la recta numérica:

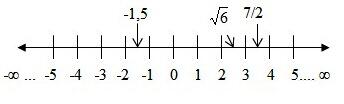
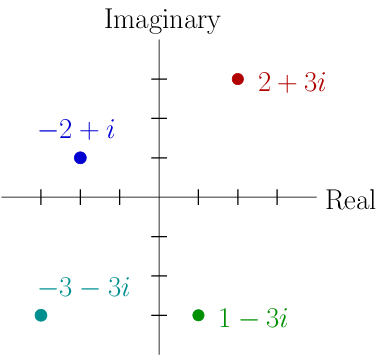
Sin embargo, los números complejos tienen dos coordenadas (una se llama parte real y la otra parte imaginaria) y por tanto no se pueden representar en una recta, sino que hay que hacerlo en un plano. Por ejemplo, en el siguiente plano se han representado cuatro números complejos: el de coordenadas (2,3), que también se escribe como 2+3i, el de coordenadas (-2,1), que también se escribe como -2+i, el número (-3,-3)=-3-3i y el número (1,-3)=1-3i.

Volvamos a nuestra ecuación ?(s)=0 (o a los ceros de la función zeta de Riemann, si os gusta más decirlo así ahora). Esta ecuación tiene infinitas soluciones. Definitivamente está claro que es más complicada que la sencilla ecuación del principio f(x)=0, que tenía solo dos soluciones. Además no olvidemos que se tratan de soluciones complejas, es decir, de puntos del plano.

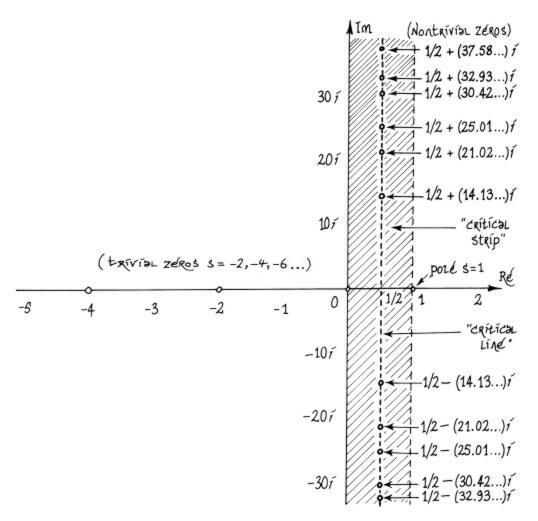
La pregunta clave es: ¿Y si representamos las soluciones en el plano, (dónde caen los ceros de la función zeta de Riemann)? La respuesta no es evidente, pues no se conocen todos los ceros de ?(s). Aparte de los llamados ceros triviales: los enteros pares negativos, o sea, los números de coordenadas (-2,0), (-4,0), (-6,0)... en el plano complejo, se sabe que el resto de los ceros (llamados ceros no triviales) han de estar necesariamente situados en la franja sombreada del gráfico de abajo, es decir, su parte entera debe estar entre 0 y 1.

Y por fin hemos llegado a poder formular la hipótesis de Riemann, que trata de afinar mucho más la franja sombreada para dar una zona más concreta de donde están los ceros. La conjetura dice así:

Los ceros no triviales de la función zeta de Riemann tienen todos parte real igual a 1/2.

Gráficamente eso quiere decir que los ceros estarían todos sobre la línea discontinua vertical dibujada arriba en el plano complejo. Si la hipótesis fuera falsa, entonces existiría algún cero no trivial fuera de esa línea (aunque dentro de la franja sombreada, eso seguro), pero de momento todos los ceros que se han encontrado (incluso con ayuda de potentes ordenadores) siempre están sobre la línea crítica. Sin embargo, hace falta una demostración matemática rigurosa que nos asegure que siempre va a ser así, y que nunca se encontrará un cero no trivial fuera de la línea crítica de números complejos con parte real igual a 1/2. (Si no tenéis claro qué es eso de una "demostración" echad un vistazo a §3.)

¿Y por qué es importante todo esto para los matemáticos? La función zeta de Riemann está fuertemente relacionada con los números primos (Euler fue el primero en darse cuenta de este hecho, §36). Entender los ceros de la función zeta de Riemann conduciría a resultados fundamentales sobre cómo están distribuidos los números primos... y no olvidemos que los números primos son los ladrillos de las matemáticas, pues todos los números compuestos pueden expresarse como producto de primos. Así, Hilbert incluyó la hipótesis de Riemann como el octavo problema de su famosa lista de problemas sin resolver a principios del s. XX, y afirmó que demostrar la conjetura de Riemann implicaría, en particular, demostrar la conjetura de los primos gemelos, §33.

La criptografía actual se basa en las matemáticas de los números primos. Cada vez que hacemos una compra por Internet o enviamos un mensaje esta información se cifra para que terceras personas no puedan acceder a ella. Si tuviéramos un conocimiento completo de cómo se distribuyen los números primos, entonces, todo el sistema de claves de la World Wide Web se derrumbaría. Las técnicas que condujeran a la demostración de la hipótesis de Riemann no solo constituirían un hito en la historia de las matemáticas, sino que podrían conllevar un cambio en la forma del cifrado de la información en un mundo cada vez más conectado. Pero por suerte, o por desgracia, parece que está más cerca el desarrollo pleno de la llamada criptografía cuántica (no basada en los números primos) que la demostración de la hipótesis de Riemann.

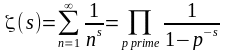
9. Los ¿perfectos? números perfectos

Los números perfectos son aquellos que se obtienen sumando sus divisores propios (o sea, sus divisores sin contar el propio número). Por ejemplo, el número 6 es perfecto porque los divisores propios del 6 son 1, 2 y 3, y sumando estos se obtiene precisamente el número 6. Los tres números perfectos más pequeños son 6, 28 y 496:

6 = 1 + 2 + 3

28 = 1 + 2 + 4 + 7 + 14

496 = 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248

Pero... ¿por qué estos números se llaman perfectos?

El origen de los números perfectos se remonta a la Escuela Pitagórica, y ya aparecen algunos resultados importantes sobre los mismos en los Elementos de Euclides, §11, probablemente recogidos de algún texto pitagórico anterior. Los antiguos griegos conocían los cuatro primeros números perfectos (el cuarto es 8128, recogido por Nicómaco de Gerasa hacia el año 100). Pitágoras y los suyos se empeñaron en darle una explicación casi religiosa a esos números. Su belleza y armonía los hacían perfectos. San Agustín afirmó que Dios hizo el mundo en 6 días porque eligió un número perfecto. El siguiente número perfecto, 28, coincide mágicamente con el ciclo lunar. Y así, a lo largo de la historia, siempre aparecía una explicación mística de los números perfectos.

Nicómaco propuso, sin demostrar, una seria de afirmaciones en relación a los números perfectos. Algunas se han revelado falsas y otras están pendientes de demostrar (aunque parecen bastante plausibles). Estas son:

• El número perfecto n-ésimo tiene n dígitos [FALSO]. Aunque los primeros números perfectos lo cumplen [el primero (6) tiene una cifra, el segundo (28) tiene dos cifras, el tercero (496) tiene tres cifras...] la afirmación es falsa para el quinto número perfecto (33550336).

• Todos los números perfectos son pares [CONJETURA]. Hasta ahora se ha encontrado medio centenar de números perfectos (los últimos tienen millones de dígitos) y todos ellos son pares. ¿Habrá alguno impar? No se sabe.

• Todos los números perfectos acaban en 6 o en 8 alternativamente [FALSO, AL MENOS PARCIALMENTE]. Es cierto que todos los números perfectos pares acaban en 6 o en 8, aunque no ocurre alternativamente. Además, si hubiera números perfectos impares, dejaría de ser cierto. La demostración para números pares se puede deducir del siguiente resultado.

• Cualquier número perfecto es de la forma 2^p-1(2^p- 1), para p > 1, siendo 2^p- 1 un número primo. [CONJETURA]. La fórmula anterior ya es mencionada por Euclides, §11. Para números perfectos pares, Euler, §36, demostró que esta afirmación sí es cierta, pero queda por demostrar que también es cierta para números perfectos impares (o bien demostrar que todos los números perfectos son pares, lo que sigue siendo una conjetura como ya se ha indicado). Por cierto, un número primo de la forma 2^p - 1 se llama primo de Mersenne y, para que 2^p - 1 sea primo, es necesario que p también sea primo.

• Hay infinitos números perfectos [CONJETURA]. Otra conjetura que nos recuerda a la conjetura de los primos gemelos, §33, que a su vez tiene mucho que ver con la difícil hipótesis de Riemann, §8.

Podríamos seguir llenando páginas y páginas con propiedades de los números perfectos. Así que se podrá discutir todo lo que se quiera sobre si estos números son divinamente perfectos o no, pero de lo que no cabe duda es de que son endiabladamente complicados.

10. Triángulos en torres eléctricas

Seguro que todos reconocéis en la foto una torre eléctrica de alta tensión, de esas que están por todas partes. Si os fijáis la próxima vez que encontréis una por lo carretera, veréis que tienen un montón de triángulos metálicos. Triángulos grandes, triángulos pequeños dentro de los grandes..., pero solo triángulos. ¿Por qué no aparecen otras formas poligonales como cuadrados o rectángulos? ¿Por qué solo triángulos?

Estas torres eléctricas deben tener una estructura estable que soporte los vientos, los cambios de temperatura o incluso movimientos de tierra moderados. Pues bien, resulta que los triángulos son los únicos polígonos "rígidos", tal y como estudió el matemático francés Augustin Cauchy a principios del siglo XIX.

Esto quiere decir que, aunque sus esquinas estén articuladas (pues la estructura se forma atornillando puntales rectos), no pueden moverse sin deformar ninguno de los lados, lo que les confiere gran estabilidad. Sin embargo, con el resto de polígonos no sucede así, como se ve, por ejemplo, en este rectángulo, que se convierte en un romboide fácilmente modificando las esquinas, pero sin deformar los lados:

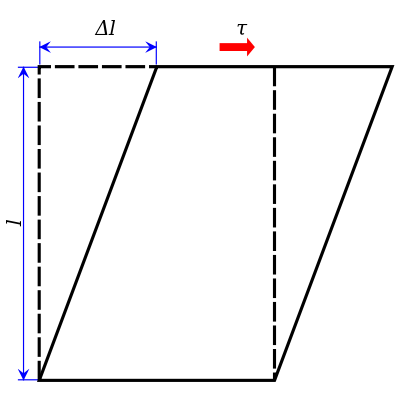
Así que una torre hecha de rectángulos (o cualquier polígono que no sea un triángulo) se derrumbaría en cuanto una esquina se aflojara un poquito...

Y no solo las torres eléctricas, muchas otras estructuras se construyen a base de triángulos para asegurar la estabilidad, como, por ejemplo, el puente de la imagen.

¿Os imagináis qué pasaría si no estuvieran las traviesas diagonales?

11. Euclides, sus Elementos y la infinitud de los números primos

Euclides, hacia el año 300 a. C., fue de los primeros que empezaron a utilizar el razonamiento matemático de forma similar a como se realiza hoy en día. Los Elementos, su obra maestra, está formada por 13 libros con 465 proposiciones (esto es, verdades matemáticas) que son demostradas con una lógica impecable a partir de una serie de postulados iniciales básicos sobre los que Euclides construye toda su obra. Y ese es su mérito: haber dado forma y estructura lógica a los resultados matemáticos que se conocían en su momento pero que solo estaban expresados de forma vaga.

Una de las técnicas utilizadas por Euclides en sus razonamientos es la conocida como "reducción al absurdo". Consiste en demostrar que una proposición matemática es verdadera probando que, si no lo fuera, conduciría a una contradicción. Vamos a verlo con más detalle.

En una demostración por reducción al absurdo hay que partir de una hipótesis contraria a lo que se quiere demostrar y, a través de una cadena de razonamientos acertados, llegar a una conclusión falsa, inconsistente o absurda. El fallo que ha conducido a esa conclusión final errónea ha de haber sido la hipótesis de partida (pues los razonamientos intermedios son acertados). Por consiguiente, queda así demostrado que la hipótesis cierta es la opuesta a la inicial (que era la contraria a lo que queríamos demostrar) y por tanto la hipótesis cierta es lo que realmente queríamos demostrar.

Entre las grandes proposiciones y teoremas, §3, que Euclides demostró magistralmente, se encuentran resultados que nos suenan a todos de las clases del instituto, como por ejemplo:

• Los ángulos de un triángulo suman 180°.

• En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos (Teorema de Pitágoras).

• Hay infinitos números primos.

Estos resultados son conocidísimos... pero ¿son realmente ciertos? Claro que sí: no nos engañaron los profesores (bueno, el de los 180° tiene más miga de la que parece, §24). Ahora bien: ¿cómo se demuestra que estas proposiciones son ciertas? ¿Sabríais vosotros demostrarlas? Mmmh... no es fácil ¿verdad? Pues Euclides lo hizo hace 2300 años (!!!).

Presentamos a continuación una demostración de la infinitud de los números primos (2, 3, 5, 7, 11, 13, 17...). La demostración es por reducción al absurdo.

Supongamos que el conjunto de los números primos es finito, siendo el primo mayor M. Así pues, escribimos ese conjunto como:

{2, 3, 5, 7, ..., M}

Consideremos el número que se forma multiplicando todos los números del conjunto anterior y sumándole 1 a dicho resultado, es decir:

2·3·5·7···M + 1

Este número que acabamos de construir es mayor que M (pues se ha multiplicado el propio M por números mayores que 1).

Como ese número es mayor que M no puede estar en el conjunto de los números primos {2, 3, 5, 7,..., M} (cuyo máximo era M). Por tanto no es primo, es decir, es compuesto.

Como el número 2·3·5·7···M + 1 es compuesto entonces puede factorizarse en números primos, es decir, tendrá en su factorización algún factor primo del conjunto {2, 3, 5, 7,..., M}.

Para mayor claridad vamos a suponer que el número compuesto 2·3·5·7···M + 1 tiene al número primo 3 en su factorización (es decir, que es divisible entre 3). El argumento que viene a continuación podría hacerse con cualquier otro número del conjunto de primos {2, 3, 5, 7,..., M} aunque no fuera el 3.

Como tiene al 3 en su factorización, podremos escribir el número 2·3·5·7···M + 1 como producto del 3 por otro número natural que llamaremos q. Esto es:

2·3·5·7···M + 1 = 3·q

Dejando el 1 a la izquierda en la igualdad obtenemos

1 = 3·q - 2·3·5·7···M

Sacando factor común el 3:

1 = 3·(q - 2·5·7···M)

Acabamos de llegar a la conclusión que el número 1 se puede poner como el producto de 3 por otro número natural (el del paréntesis), lo que es absurdo: ¡1 no puede ser menor que el resultado de multiplicar 3 por algo! Nótese que sería igualmente absurdo si en vez de con el 3 lo hubiéramos hecho con el 5 o el 7 o cualquier otro primo del conjunto {2, 3, 5, 7, ..., M}.

Como los razonamientos que hemos ido haciendo son todos correctos, lo único que explica que hayamos llegado a una conclusión absurda (errónea) es que la hipótesis de partida no fuera correcta.

Por lo tanto, la hipótesis correcta tiene que ser la contraria de aquella con la que iniciamos la demostración, es decir, la hipótesis correcta es que el conjunto de los números primos NO es finito (o sea, que es infinito). QED.

Por cierto, QED significa quod erat demonstrandum, y se suele poner cuando termina una demostración más o menos larga, por si alguno está tan perdido que ni se ha enterado de que ha llegado al final de la prueba del teorema.

12. Números agujeros negros

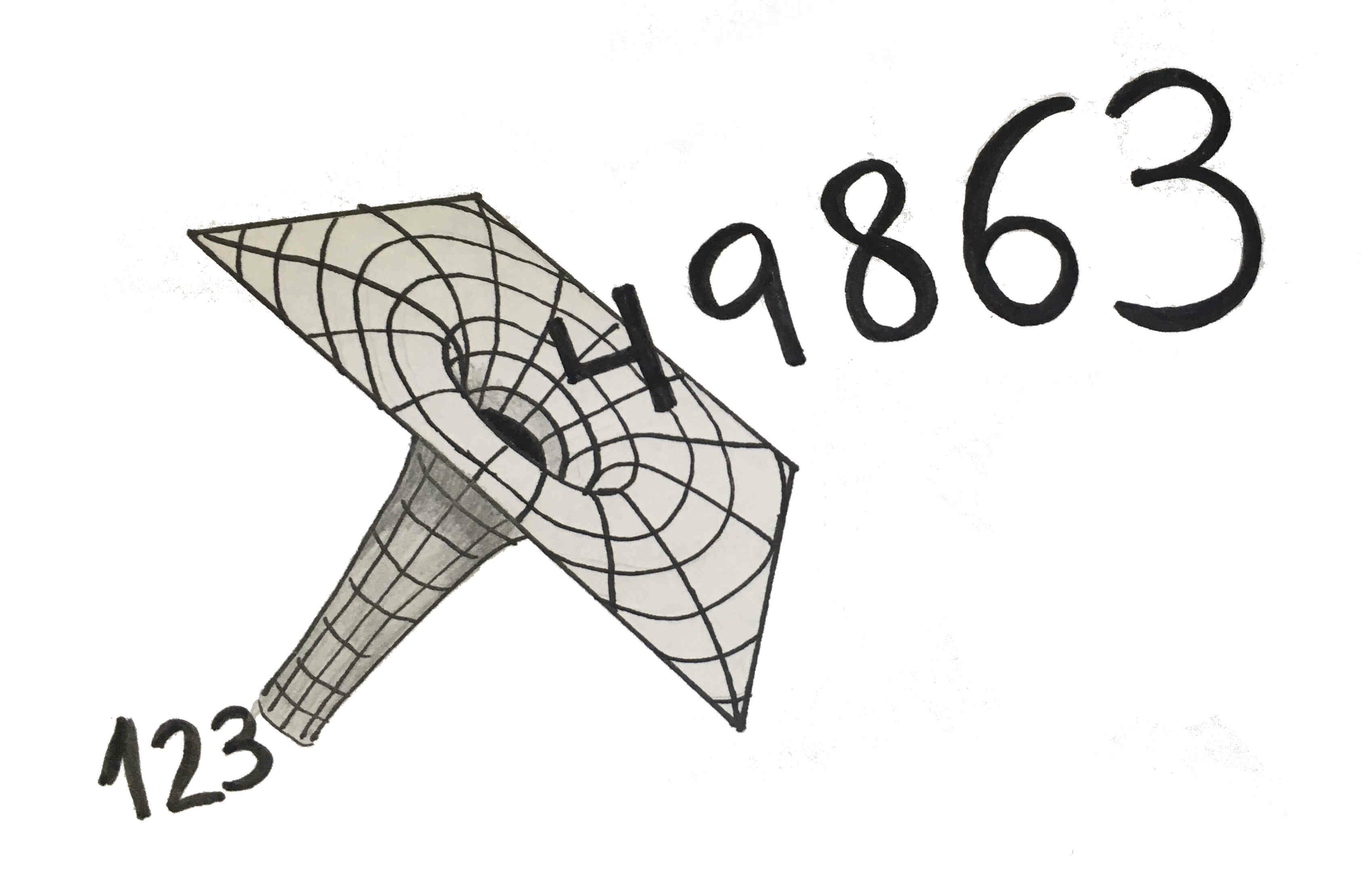
Los agujeros negros son objetos del espacio-tiempo tan densos que no dejan escapar ni tan siquiera la luz. Atrapan todo lo que hay a su alrededor. Pues bien, también hay números que se comportan así: atraen a todos los demás números hacia ellos.

El número 123 es uno de esos agujeros negros numéricos. Vamos a ver por qué. Tomamos un número natural cualquiera de tres o más cifras y contamos cuántas de ellas son pares y cuantas impares, y con estos datos construimos un número de la siguiente forma: colocamos primero la cantidad de cifras pares que tenía el inicial, después la cantidad de cifras impares y después la cantidad total de cifras que tenía. Con el número obtenido hacemos lo mismo, y así sucesivamente. Sea cual sea el número inicial siempre terminaremos en el 123, y no saldremos de él.

Por ejemplo, pensemos en el número 49863. Tiene 3 cifras pares (el 4, el 8 y el 6) y 2 impares (el 9 y el 3). Como tiene 5 cifras, con él obtendríamos el número 325. Hacemos lo mismo con éste: 1 dígito par (2) y 2 impares (3 y 5). Como tiene 3 cifras, obtenemos con él el 123. Y ahora el 123 tiene una par (el 2), dos impares (el 1 y el 3) y tres dígitos, obteniendo así el número 123 de nuevo. Por tanto el 123 se ha tragado al 49863 como si fuera un agujero negro.

13. La ecuación cúbica: de traca

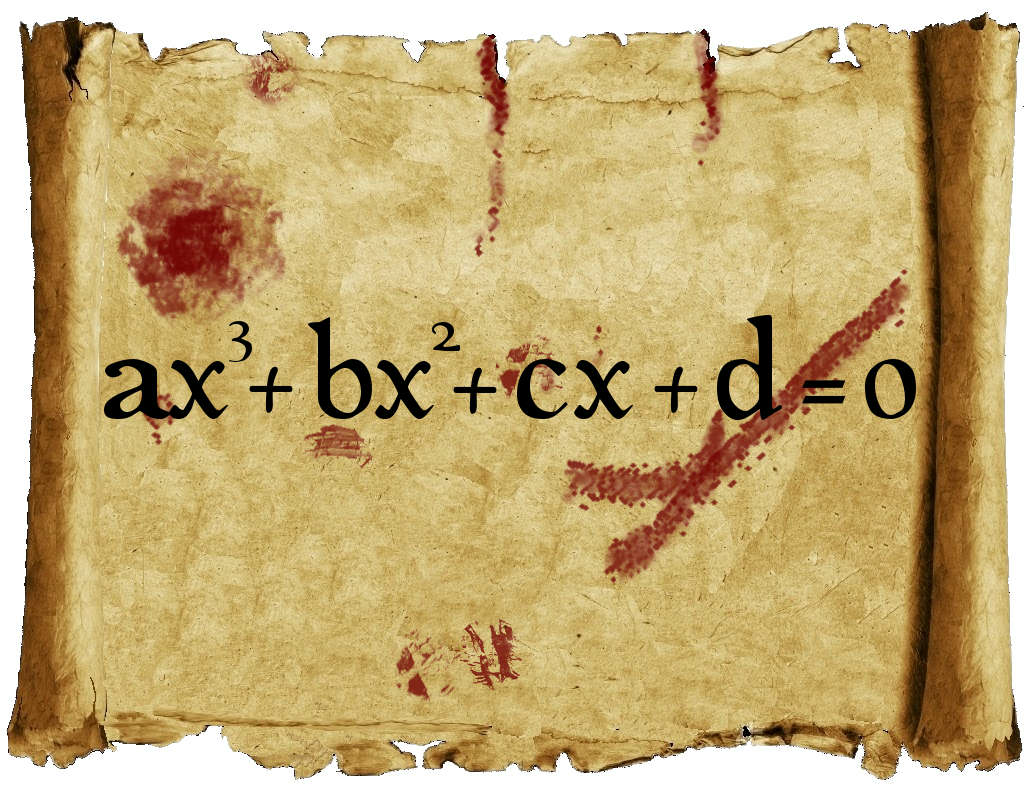
Hablando mal y pronto podemos decir que resolver una ecuación es encontrar los valores de x que hacen que se cumpla la igualdad. Por ejemplo, para la ecuación 4x² ? 3x ? 10 = 0 tenemos que las soluciones son x = 2 y también x = ?5/4. Vemos que al cambiar la x por el valor 2 se cumple la igualdad. Y lo mismo pasa para x = ?5/4. Esta ecuación es de segundo grado porque lleva x² (los matemáticos las llaman ecuaciones cuadráticas) y para obtener las soluciones anteriores basta aplicar la fórmula que seguro que habéis estudiado alguna vez en el instituto... esa de:

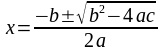
donde a es el número que aparece delante de la x², b es el número que aparece delante de la x, y c es el número suelto. O si queréis hablar un poco mejor, son los coeficientes del término cuadrático, del término lineal y el término independiente. En nuestro caso: a = 4, b = ?3, c = ?10. Con la fórmula anterior podemos resolver cualquier ecuación de 2º grado poniendo en lugar de a, b, c los valores que correspondan.

Esa fórmula se conoce desde hace muchos muchos años. Tantos que no se sabe ni quién fue el primero en usarla. La fórmula es muy bonita, pero no es la panacea, porque solo vale para ecuaciones de segundo grado. ¡Ajá!, ¿y qué ocurre con las ecuaciones de tercer grado, es decir, las que llevan incluso un término con x³ y que los matemáticos llaman ecuaciones cúbicas?

Pues nada, porque por suerte hay otra fórmula, que también es muy chula, pero que no la vamos a escribir porque es un poco larga. ¿Y se sabe quién descubrió esa fórmula? Mmmh, sí que se sabe y la historia no tiene desperdicio. Varios son los culpables.

Empecemos por Scipione del Ferro. Este matemático italiano de la Universidad de Bolonia fue el primero en encontrar un método para resolver ecuaciones cúbicas del tipo que llaman deprimidas, que son las que no llevan x², como por ejemplo 2x³ + x ? 7 = 0.

Del Ferro, en vez de lanzarse como loco a publicar este importante hallazgo, prefirió guardarse la "fórmula" en secreto. ¿Por qué? Bueno, porque era el año 1500 más o menos y entonces los conocimientos se reservaban para poder usarlos como armas arrojadizas contra otro matemático: "Mira lo que sé yo, anda, si quieres quitarme la plaza en la universidad tendrás que saber tanto como yo". No había oposiciones por aquella época y las cátedras eran tan golosas como ahora. Otras veces se enfrentaban en estos retos por el dinero que sacaban de las apuestas. En ambientes académicos eran casi como las finales de fútbol de ahora. Un espectáculo.

Por cierto, que hemos puesto entre comillas la palabra "fórmula". Hay que tener en cuenta que el lenguaje algebraico estaba empezando a dar sus primeros pasos por aquel entonces, y más que fórmulas eran "recetas" dichas de palabra: "coge el número tal y hazle tal operación, después súmale..." Además, solían considerar solo números positivos en busca siempre de interpretaciones geométricas.

Total, que el bueno de del Ferro se guardó su secreto hasta casi el lecho de muerte, y solo se lo confesó entonces a uno de sus alumnos. Tal vez debió de pensar que en la tumba de poco le iba a servir. El alumno, bastante mediocre como se verá después, se llamaba Antonio María Fior.

En cuanto Fior empezó a alardear de conocer la fórmula se organizó una contienda matemática entre él y nada menos que Tartaglia, uno de los grandes matemáticos del Renacimiento y experto en este tipo de duelos.

Antes de seguir, conviene decir en honor de Tartaglia que su nombre verdadero era Niccolo Fontana, pero se quedó con el apodo de Tartaglia (tartaja, tartamudo) desde que de niño sufrió una herida de sable en la cara durante la invasión francesa de su ciudad natal de Brescia (Italia) que le ocasionó un defecto en el habla. Peor suerte corrió su padre que murió en la batalla. Cosas de la época. Pero volvamos al duelo.

Antonio Fior partía como favorito gracias a su fórmula secreta para resolver ecuaciones cúbicas deprimidas. Cada uno de los combatientes propuso al otro 30 problemas matemáticos que debían ser resueltos el 13 de febrero de 1535. Fior eligió 30 ecuaciones cúbicas deprimidas para "lanzarle" a Tartaglia, mientras que Trataglia le propuso 30 problemas variados. El que ganara se llevaría el dinero de la apuesta y el prestigio. Ganó Tartaglia 30-0. Y es que Tartaglia, que al principio solo sabía resolver ecuaciones cúbicas sin el término lineal (como, por ejemplo, 2x³+4x²?5=0), debía haber conseguido también aprender a resolver ecuaciones cúbicas deprimidas (sin el término cuadrático) en algún momento previo.

Y todavía hay más. En medio de esta locura matemática aparece el más excéntrico de todos los matemáticos: Gerolamo Cardano. Astrólogo, jugador empedernido y médico de reconocido prestigio, fue acusado en Bolonia de herejía en 1570. Hijo ilegítimo de infancia enfermiza, se cuenta de él que gustaba de inflingirse dolor a sí mismo, que orinaba litros y litros cada día, que era insomne, que predecía el futuro o que nació muerto, pero que volvió a la vida tras bañarse en vino. Su mujer fue envenenada por su propio hijo, que fue subsiguientemente ejecutado. En fin, más cosas de la época.

El caso es que tras el abrumador triunfo de Tartaglia en el famoso duelo con Fior, Cardano invita al flamante ganador a su casa con la promesa de ayudarle a salir de sus continuos apuros económicos, y le pide a cambio que por favor le cuente cómo resolver ecuaciones cúbicas deprimidas. Cardano jura solemnemente a Tartaglia guardar el secreto y este acaba cediendo tras muchas presiones del obsesivo médico.

Con el método para resolver ecuaciones cúbicas deprimidas (o sea, sin la x²), Cardano es capaz ya de resolver ecuaciones cúbicas totalmente generales (como, por ejemplo, x³+x²+x+1=0), pues había encontrado una forma de transformar estas ecuaciones generales en otras deprimidas. Pero se ve imposibilitado para publicar sus resultados, pues la solución pasa por reducirlas a ecuaciones deprimidas. Aunque el excéntrico matemático y médico no tenía problemas económicos, y se encontraba en una posición cómoda para permitirse el lujo de publicar resultados (no como el pobre Tartaglia, que había de ganarse las habichuelas a base de duelos matemáticos), la promesa hecha a Tartaglia lo ataba de pies y manos.

Sin embargo, Cardano, ansioso por publicar, encuentra una salida. Sostiene que la solución de la ecuación cúbica deprimida que utiliza en su resolución de la ecuación general no es la de Tartaglia, sino la de del Ferro. Es posible que el manuscrito original de del Ferro hubiera sido heredado por su yerno Annibale Nave (quien reemplazó a del Ferro como catedrático en la Universidad de Bolonia) y que finalmente acabara en las manos de Cardano, liberándole de la promesa a Tartaglia, porque al fin y al cabo ahora tenía unas fuentes alternativas. Cardano publica los resultados en su libro Ars Magna en 1545.

Tartaglia arde de rabia al enterarse de la afrenta de Cardano y comienza una gran pelea dialéctica entre ellos, insultos incluidos. Le escribe cartas encendidas a Cardano, que se niega a contestar directamente, dejando la correspondencia en manos de su secretario Ludovico Ferrari.

¿Y este qué pinta en la historia? Pues mucho. Resulta que Ferrari llega con 14 años a casa de Cardano como sirviente. Su interés por los trabajos del prestigioso médico y matemático van en aumento, de ese modo Ferrari pasa así de sirviente a secretario, de secretario a alumno, y finalmente de alumno a colega del propio Cardano. El nivel matemático de Ludovico Ferrari supera a su maestro y llega a resolver ecuaciones cuárticas generales (con x⁴ también) con un método que consiste en reducirlas otra vez a ecuaciones cúbicas deprimidas. De hecho, la demostración de Ferrari apareció también en el Ars Magna.

En 1548, Tartaglia recibe una oferta para dar clases en Brescia. Al fin una oportunidad para salir de su mala racha. Pero a Tartaglia le quedaba un último reto pendiente para poder optar a la plaza: debía combatir con Ferrari sobre las ecuaciones de tercer y cuarto grado. El 10 de agosto de 1548 se produce el asalto y, esta vez, el genial Tartaglia se ve superado por su adversario, perdiendo así sus últimas esperanzas de prosperidad. Murió igual de pobre que nació.

La verdad es que Ferrari tampoco acabó sus días muy bien que digamos. Justo el año en que se le ofreció la plaza en la Universidad de Bolonia (1565) murió envenenado con arsénico, probablemente a manos de su propia hermana. En cuanto a Cardano, puede decirse que creyó a muerte en la astrología, cuyas cábalas predecían que el día de su muerte sería el 20 de septiembre de 1576. Se cuenta que se suicidó ese día para hacer correcta la predicción.

Y después de este culebrón ya sabemos al menos que hay métodos para resolver ecuaciones generales no solo de grado 3, sino incluso de grado 4. Las fórmulas son bastante largas como para ponerlas aquí, pero lo importante es que existen. Ahora bien, ¿qué pasa con las ecuaciones de grado 5?

Pues para eso hay que esperar hasta el siglo XIX, cuando un matemático noruego (Abel) y otro francés (Galois) demostraron que las ecuaciones quínticas generales (con x⁵) no tienen fórmula algebraica para resolverlas (hablando un poco mejor: no son resolubles por radicales). Y de hecho se deduce de sus resultados que tampoco puede haber un método exacto para las ecuaciones generales de mayor grado.

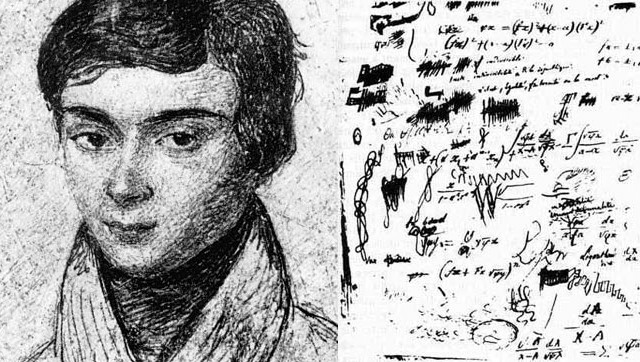
Por cierto, que Abel murió jovencísimo de tuberculosis, con 26 años... aunque la traca final de toda esta historia es para Galois que murió, con tan solo 20 años, de las heridas causadas por un duelo a pistolas (un duelo de verdad, por un asunto de faldas, nada que ver con los duelos académicos de Tartaglia y cía.). Suerte que la noche de antes se dedicó a escribir buena parte de sus grandes aportaciones matemáticas en una correspondencia arrebatada, que ha quedado como legado de uno de los mejores matemáticos de todos los tiempos pese a su brevísima vida.

14. Pares o nones: el triángulo de Sierpinski y el de Pascal

El triángulo de Sierpinski se forma siguiendo el proceso de la imagen de arriba una y otra vez hasta el infinito. Esa forma repetitiva es lo que se llama un fractal. Más concretamente se construye así:

1. Se empieza con un triángulo equilátero.
2. Se divide en 4 triángulos equiláteros iguales y se quita el central.
3. Se repite el paso anterior con cada uno de los triángulos que quedan... y así infinitamente.

Por otra parte, el triángulo de Pascal está formado por filas de números, siendo los laterales siempre el 1 y obteniéndose los demás números como suma de los dos superiores como se ve a continuación para las primeras filas (habría infinitas):

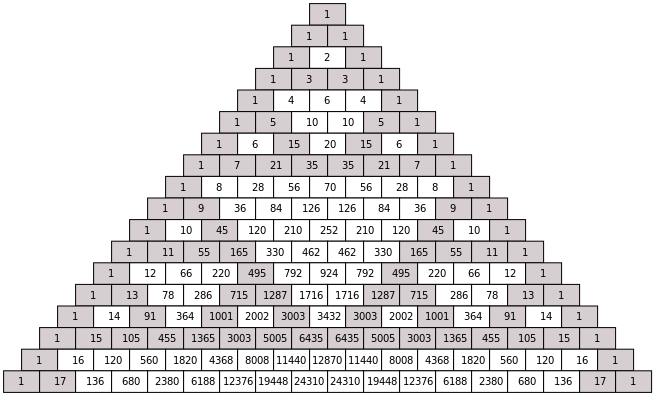
La pregunta que nos interesa aquí es ¿qué números son más frecuentes en el triángulo de Pascal: los pares o los impares? Y de paso, ¿qué tiene que ver el triángulo de Pascal con el de Sierpinski?

En la imagen anterior del triángulo de Pascal se han sombreado los números impares mientras que los pares se han dejado en blanco. Se aprecia un cierto patrón, que recuerda a la construcción del triángulo de Sierpinski que vimos al principio. Es más, si nos fijamos con detalle en el triángulo de Sierpinski veremos que tiene exactamente la misma forma que el triángulo de Pascal, donde los números pares se han pintado en blanco y los impares de gris.

Así que, volviendo a la pregunta: ¿Hay más pares o más impares? Pues la respuesta ahora empieza a estar clara y el resultado es sorprendente. Son "casi todos" pares (blancos). De hecho, conforme el triángulo de Pascal se va ampliando a más y más filas, la probabilidad de encontrarse un número par tiende a 1 (o sea, al 100%) mientras que la probabilidad de encontrarse un número impar tiende a 0. ¿Veis cómo las zonas blancas (números pares) en cada iteración se van "comiendo" las zonas grises (números impares)?

Ah, y por si a alguien le suena otro nombre, el triángulo de Pascal es también conocido como triángulo de Tartaglia, o triángulo de Khayyam, o triángulo de Yang-Hui, dependiendo del país, pues diferentes culturas lo han estudiado en detalle. Y por otra lado el triángulo de Sierpinski se llama también criba de Sierpinski o estuche de Sierpinski.

15. Conjuntos de Julia

Una función puede verse como una especie de máquina en la que entran valores (que solemos denotar por x) y, tras una serie de operaciones, salen otros valores [que llamamos y o f(x)]. A cada entrada x le corresponde una salida y concreta de acuerdo a la función. A los matemáticos franceses Pierre Fatou y Gaston Julia (s. XX) se les ocurrió estudiar la siguiente cuestión aplicada a cierto tipo de funciones: ¿y si el valor de salida lo vuelvo a meter en la función como nueva entrada y repetimos esto así cíclicamente? El resultado es sorprendentemente bello: se obtienen imágenes como la anterior, que los matemáticos llaman fractales.

Empecemos con una función sencilla: f(x)=x². Se trata de una "máquina" que eleva al cuadrado el valor de la entrada. Así, por ejemplo, vamos a empezar metiendo el número 2 a la función (ese primer número con el que empezamos se llama semilla). Como la función calcula el cuadrado, el resultado de salida será un 4. Si ahora cogemos ese 4 y lo metemos a la entrada de la función nos dará 16. Y ahora podríamos coger el 16 y meterlo otra vez a ver qué sale, y así una y otra vez. Matemáticamente podríamos escribir todo esto de la siguiente manera:

f(2)=4

f(4)=16

f(16)=256

f(256)=65536

...

Otra forma de expresar lo anterior es mediante una serie, que empieza en la semilla y sigue con las salidas que nos da la función:

2, 4, 16, 256, 65536, ...

Es evidente que nos van a ir saliendo números más y más grandes. Se dice entonces que la serie anterior es una serie divergente. ¿Qué ocurriría si en vez de con el número 2 empezamos con otro semilla? ¿Vamos a obtener siempre una serie divergente? Probemos con otro número. Por ejemplo, con la semilla 0.5 tendríamos: f(0.5)=0.25, f(0.25)=0.0625, etc... Se ve más claro en forma de serie:

0.5, 0.25, 0.0625, 0.00390625, ...

Es decir, en este caso los números no se hacen cada vez más grandes como ocurría antes y podemos afirmar que si partimos de la semilla 0.5 se tiene ahora una serie no divergente. Así que acabamos de ver que hay semillas (por ejemplo x=2) que nos dan series divergentes y otras semillas (por ejemplo x=0.5) que no. La pregunta clave es ¿para qué semillas vamos a obtener series no divergentes? Si lo pensamos bien veremos que, si la semilla toma cualquier valor entre ?1 y 1, tendremos series no divergentes. Podéis hacer la prueba eligiendo cualquier semilla que esté en el conjunto de los números entre ?1 y +1 (recuerda que los números negativos al elevarlos al cuadrado dan resultados positivos).

Vale, ¿pero qué tiene que ver esto con el extraño dibujo de arriba, o sea, con los conjuntos de Julia? Bueno, para verlo tenemos que complicarlo un poco. En vez de trabajar con números reales, vamos a trabajar con números complejos (ya hemos hablado en §8 sobre los números complejos al comentar la hipótesis de Riemann). Usaremos en adelante la letra z en vez de x, porque esa es la notación habitual para los números complejos. También vamos a modificar la función: ahora, además de elevar al cuadrado, vamos a restar una unidad, es decir, la nueva función compleja que nos interesa es:

f(z)=z²-1.

La pregunta es la misma de antes: ¿para qué semillas vamos a obtener series no divergentes? Eso sí, ahora hay que tener en cuenta que las semillas son números complejos y, por tanto, tienen dos coordenadas y gracias a ello las podemos representar en el plano complejo. Eso es precisamente lo que se ha hecho en el dibujo de arriba para la función f(z)=z²-1: se han pintado en color negro los puntos del plano que corresponden a semillas que dan series no divergentes y se han dejado en blanco el resto de puntos que sí dan series divergentes (no se han señalado los ejes de coordenadas del plano complejo). Al conjunto negro se le llama conjunto de Julia y al blanco se le llama conjunto de Fatou.

Hay que recordar que la suma de números complejos se define coordenada a coordenada como:

(a, b) + (c, d) = (a+c, b+d),

mientras que la multiplicación de números complejos se define de forma un poco más complicada mediante la expresión:

(a, b) · (c, d) = (ac?bd, ad+bc).

Por ejemplo, si empezamos con la semilla de coordenadas complejas (1,1) obtendríamos para la primera salida de f(z)=z²-1 lo siguiente:

(1, 1)² ? 1 = (1, 1) · (1, 1) ? (1, 0) = (1?1, 1+1) ? (1, 0) = (0, 2) ? (1, 0) = (?1, 2)

Utilizando este número como nueva entrada obtendríamos ahora:

(?1, 2)² ? 1 = (?1, 2) · (?1, 2) ? (1, 0) = (1?4, ?2?2) ? (1, 0) =

= (?3, ?4) ? (1, 0) = (?4, ?4)

Podemos continuar y obtener así la siguiente serie divergente para la semilla (1, 1):

(1, 1), (?1, 2), (?4, ?4), (?1, 32), (?1024, ?64), (1044479, 1310721), ...

Así pues, el punto del plano complejo (1, 1) lo pintaríamos en blanco, pues pertenece al conjunto de Fatou.

Sin embargo, para la semilla (0.1, 0.2) obtendríamos una serie que no diverge. Representamos las primeras iteraciones con una aproximación hasta la cuarta cifra decimal:

(0.1, 0.2), (?1.03, 0.04), (0.0593, 0.0824), (?1.3273, -0.0098), (0.7617, 0.0259), ...

Entonces el punto (0.1, 0.2) lo pintaríamos en negro, pues pertenece al conjunto de Julia.

Este mismo procedimiento que hemos hecho con dos puntos (semillas) podríamos repetirlo con cientos o miles de puntos del plano con la ayuda de un ordenador, que realice los cálculos y decida si hay que pintarlos blancos (diverge) o negros (no diverge).

Para otras funciones distintas también podemos estudiar los conjuntos de Julia y obtener gráficos tan llamativos como el siguiente para la función f(z)=z²-c, donde c=(?0.8, 0.156):

¿Los colores? Muy fácil: no todas las series divergen igual de rápido. Simplemente se ha establecido una gradación en el color según la rapidez con la que divergen.

16. Pi: ¿un número simplemente normal?

Richard P. Feynman recibió el premio Nobel de Física en 1965 por sus aportaciones a la electrodinámica cuántica, aunque este genial e imaginativo físico también era capaz de pasar una noche entera debatiendo por qué un spaguetti se parte en tres trozos -y no en dos- al doblarlo con los dedos por sus extremos... Fue además un excelente divulgador, un amante de la samba brasileña, un amateur de los bongos y una personalidad única.

Feynman bromeaba con que le gustaría aprender las cifras del número ?=3,141592... hasta la posición 767, porque así los últimos dígitos que recitaría serían 999999, con lo que parecería que pi fuera un número periódico mixto. Pero sabemos que no lo es: ? es irracional (infinitos decimales no periódicos), aunque a veces se dan casualidades y aparecen secuencias curiosas, como varios números iguales seguidos. Claro, como ? tiene infinitos decimales, no nos sorprende que pasen estas rarezas. ¿Habrá, pues, un momento en que salgan, digamos, mil números 9 seguidos?

Hoy en día se conocen billones y billones de cifras decimales del número ?. En ellas probablemente no se dé la casualidad de que aparezcan mil números 9 seguidos como dijimos antes pero quizá mucho más adelante en la serie sí que ocurra. O no. La verdad es que no se ha conseguido demostrar. La clave es una propiedad llamada normalidad.

Los matemáticos dicen que un número decimal irracional es "simplemente normal" si sus dígitos aparecen uniformemente distribuidos en el sentido de que, en promedio, la frecuencia de encontrar cada dígito del 0 al 9 es de 1 sobre 10, la frecuencia con la que aparecerá cada pareja del 00 al 99 es de 1 sobre 100, etc.

Pues resulta que a día de hoy no hay una demostración satisfactoria de que ? sea normal (ni de que no lo sea), aunque hay indicios que apuntan a que pi sería normal. Y es que demostrar cosas que tienen que ver con el infinito puede ser muy difícil (§3, §9, §29, §33), aunque a veces a algún genio se le ocurre la manera (§11).

Por otra parte es interesante escribir el número ? en binario (base 2); empezaría así:

11, 00100 10000 11111 10110 10101 00010...

Igual que podemos pasar cualquier número decimal a lenguaje binario, podemos también pasar cualquier palabra o frase a ceros y unos, y viceversa. Es lo que hacen los ordenadores con el código ASCII (de esto volveremos a hablar en §28). Por ejemplo, la palabra HOLA se escribe en binario como 01101000011011110110110001100001.

Si Feynman se preguntaba por la secuencia formada por un mismo número repetido varias veces, nosotros podríamos preguntarnos por otra secuencia que nos llame la atención, como, por ejemplo, por la anterior correspondiente a la palabra HOLA. ¿Aparecerá en el número ??... ¿Y el Quijote entero, se dará la casualidad de que esté escrito en el número ?, palabra a palabra sin perder ni una coma?

Aquí va una tanda de preguntas y respuestas por si todavía os quedan dudas:

¿Aparecen en algún momento una secuencia de seis números 9 seguidos en la expresión decimal de pi? Sí, la primera vez entre los decimales en las posiciones de la 762 a la 767. A ese lugar de ? se le llama "punto de Feynman".

¿Es ? "normal"? No lo sabemos. Todo apunta a que sí, porque sus primeros millones de decimales están distribuidos muy uniformemente (o sea, muy al azar), pero no hay una demostración válida todavía. Hace falta un enfoque más ingenioso que comprobar millones de decimales (porque millones comparado con los infinitos decimales de pi no es nada) y de momento a nadie se le ha ocurrido ese enfoque ingenioso.

¿Era Feynman "normal"? No, era un genio irrepetible.

¿Tiene el número ? infinitos decimales? Sí.

¿Aparece cada uno de los dígitos del 0 al 9 infinitas veces en la expresión del número ?? No lo sabemos, aunque todo apunta a que sí.

¿Hay algún momento en que aparezcan mil números 9 seguidos en la expresión de ?? No se sabe, aunque, si ? fuera normal, seguro que ocurriría y, de hecho, nos encontraríamos con infinitas secuencias de mil números 9. A la pregunta de si un dígito aparecerá mil veces en posiciones consecutivas se le conoce como "cuestión de Brouwer".

¿Un número irracional es necesariamente normal? No; por ejemplo, el número 1,01001000100001000001... es irracional, pero no normal (basta ver que la secuencia 11 no aparece ni siquiera una vez).

¿Contiene el número ? la palabra HOLA expresada en código ASCII binario? Sí, eso ocurre por primera vez en la posición 341373.

¿Contiene el número ? todos los textos escritos en la historia de la literatura, carácter a carácter, perfectamente ordenados en algún lejano lugar de su infinita expresión decimal? Si ? es un número normal (y estamos diciendo que eso es lo más plausible), entonce sí. Una idea similar aparece en los relatos de La biblioteca universal de Lasswitz (1901) y en La biblioteca de Babel de Borges, §32, (1941).

17. P versus NP

P versus NP es uno de los siete "problemas del milenio", §26, y la recompensa por resolverlo es de 1 millón de dólares. Es, posiblemente, el más fácil de entender de los siete... así que merece la pena intentarlo. Tiene que ver con la complejidad para resolver distintos tipos de problemas. Hay problemas que con unas pocas cuentas salen rápido (los llamados problemas tipo P), mientras que hay otros que parece que requieren muchas más cuentas (los llamados problemas tipo NP). Pero, claro, todo esto habrá que explicarlo un poco mejor...

Empecemos con un ejemplo sencillo. Imaginad que tenemos 5 cartas numeradas del 1 al 5. En principio están barajadas y lo que queremos es ordenarlas en sentido ascendente, es decir: 1, 2, 3, 4 y 5. Hay dos algoritmos o métodos que a uno se le ocurren, así, a primera vista para conseguirlo:

Método 1: Vamos pasando las cartas del mazo hasta que aparece el número 1. Entonces la sacamos del montón y la ponemos boca abajo aparte. Ahora buscamos la carta número 2 en el montón de cuatro cartas que queda: la sacamos y la ponemos aparte detrás de la 1. Nos quedan ya tres cartas solo. Buscamos la número 3 y la sacamos del montón. Y luego lo mismo para la 4 y la 5.

¿Cúanto tiempo nos llevaría esto? No mucho, ¿verdad? Por hacer un poco de cuentas, vamos a suponer que cada vez que miremos una carta del montón eso nos lleve un segundo. Cuando buscamos la carta número 1 en el mazo, nos puede aparecer justo la primera (1 segundo de tiempo), pero también podemos tener mala suerte y que se encuentre la última, o sea, que tendríamos que descubrir y mirar las 5 cartas: 5 segundos. Pues vamos a ser pesimistas y ponernos siempre en el peor de los casos, y que la carta que buscamos aparezca la última. Ya tenemos la carta número 1 fuera. Nos quedan 4 cartas, así que para encontrar la siguiente, la carta número 2, vamos a necesitar 4 segundos. Cuando la quitemos, nos quedarán 3 cartas (3 segundos), luego 2 cartas (2 segundos) y vamos a poner 1 segundo más para la última, la número 5. En este escenario pesimista habremos necesitado en total:

5 + 4 + 3 + 2 + 1 = 15 segundos.

Es poco, pero ¿y si tuviéramos más cartas que ordenar? Por ejemplo, para 20 cartas necesitaríamos más tiempo. En concreto:

20 + 19 + 18 + 17 + ... + 1 = 210 segundos.

Eso ya son 3 minutos y medio. Lógico: cuanto más cartas, más tiempo. En general para un número N de cartas tendríamos que calcular la suma:

N + (N-1) + (N-2) + (N-3) + (N-4) + ... + 1.

Con letras también se pueden hacer cuentas (es eso del álgebra y los polinomios y esas cosas del instituto). De hecho, la expresión anterior se puede simplificar, porque corresponde a una progresión aritmética y da al final

(N²+N)/2.

Ahora no vamos a ponernos aquí a repasar cómo se hacía esto de las progresiones. Para el caso, lo que nos interesa es que se trata de un polinomio en N (en el instituto casi siempre se usaba la letra x para los polinomios, pero vamos, que es lo mismo). Si cambiamos la N por 5 cartas, nos sale (N²+N)/2 = (5²+5)/2 = 30/2 = 15 segundos y, si cambiamos la N por 20, nos da (20²+20)/2 = 420/2 = 210 segundos. ¡Bien, todo cuadra con lo de antes!

Como la expresión (N²+N)/2 que nos da el tiempo de este método 1 es un polinomio, se dice que es un algoritmo de tiempo polinomial.

Método 2: Otra forma de ordenar las cartas (supongamos, como antes, que tenemos 5 para empezar) es simplemente barajarlas y probar si tenemos suerte, y que justo se nos hayan quedado ordenadas del 1 al 5. La verdad es que eso sería mucha casualidad. Si no salen en orden a la primera (como es de esperar), podemos volver a barajar y probar suerte otra vez. Y así hasta que suene la flauta. Para hacer las cuentas del tiempo que tardaríamos, vamos a suponer que nos lleva 1 segundo barajar y que además cada vez que barajamos sale una ordenación distinta. Por ejemplo, una vez puede salir el orden 2-3-5-1-4, a la siguiente el orden 4-5-2-1-3, luego 1-2-3-5-4 (uy, casi), etc... Y, como somos muy pesimistas, vamos a ponernos otra vez en el peor de los escenarios. Supongamos que nos salga la configuración 1-2-3-4-5 al final, tras haber probado todas las demás opciones. Uf, ¿y cuántas ordenaciones de la forma ×-×-×-×-× hay? Pues en el primer hueco × podemos poner 5 posibilidades (cualquiera de los 5 números posibles); en el segundo, 4 (si hemos puesto, por ejemplo, el 2 en el primer hueco ya solo nos quedan 4 opciones: 1, 3, 4 o 5); en el tercero, 3; en el cuarto, 2 y en el quinto, 1 (el número que nos quede). En total hay que multiplicar las posibilidades para obtener todas las combinaciones posibles:

5·4·3·2·1

Esto se puede escribir como 5!, donde el signo ! se lee factorial (y sí, son las famosas permutaciones de 5 elementos del instituto). En fin, que, si hacéis las multiplicaciones de arriba, os van a dar 120 segundos (2 minutos). Este método 2 es peor que el método 1 (2 minutos frente a 15 segundos para 5 cartas), pero bueno, dos minutos tampoco es tanto, ¿no? Pero si en vez de 5 cartas tenemos N cartas, tardaremos N! segundos. Por ejemplo, para el mazo de 20 cartas de antes (3 minutos y medio en el método 1) tardaremos ahora

20! = 20·19·18·17·16 · ... · 1

¿Cuánto es eso? Pues, en notación científica (uf, otra vez a hacer memoria de las clases del instituto), eso es, más o menos,

2,4·10¹⁸ segundos

¿Y para los que no son fans de la notación científica? ¿Eso es mucho? Pues un poquito: unas 5 veces la edad del universo, o sea, miles de millones de años. ¡Ni aunque hubiéramos empezado a barajar justo con el Big Bang, habríamos conseguido ordenar las 20 cartas! Es verdad que nos hemos puesto en el caso más desfavorable y que a lo mejor resulta que a la mitad nos aparece ya la ordenación buena. En cualquier caso siguen siendo miles de millones de años... Aunque siempre puede ocurrir que baraje la persona con más suerte del mundo y que justo a la primera... ¡bingo!, del 1 al 20 en un segundo. A ese ser con suerte sobrenatural los matemáticos le llaman máquina de Turing no determinista y, como os podéis imaginar, en realidad no existe, es solo una entelequia. Lo que está claro es que para el común de los mortales N! es un tiempo que nada tiene que ver con la expresión polinomial del rápido método 1. Por el contrario, este nuevo método 2 requiere un tiempo no polinomial (salvo para la envidiable máquina de Turing no determinista que podría resolverlo en tiempo polinomial). Se dice que este algoritmo es del tipo NP (del inglés: Non-deterministic Polynomial time). Los algoritmos NP son lentísimos -en seguida sobrepasamos la edad del universo-, pero, una vez que tenemos la solución, son fáciles de comprobar: en un abrir y cerrar de ojos cualquiera podría comprobar que la ordenación encontrada por la perfecta máquina de Turing no determinista es la correcta: 1, 2, 3, ..., 20.

En fin, que podemos olvidar del lentísmo método 2 y quedarnos con el método 1, mucho más eficiente. Podemos decir entonces que el problema de ordenar una baraja de cartas puede resolverse en tiempo polinomial (gracias al método 1) y referirnos a él como a un problema del tipo P.

Suerte que se nos ocurrió el método 1 ¿no? Pero eso no siempre sucede. Hay otros problemas para los que nadie ha dado con un algoritmo de resolución en tiempo polinomial; solo sabemos de ellos que pueden ser virtualmente resueltos en tiempo polinomial por máquinas de Turing no deterministas, pero eso en la práctica no se puede hacer, porque las máquinas de Turing no deterministas ya dijimos que son entelequias. Estos problemas se dice que están en la clase de complejidad NP. Y, aunque pueda parecer un lío, si lo pensáis bien, veréis que todos los problemas del tipo P son también NP, puesto que, si un simple mortal (o un ordenador real, que los matemáticos llaman máquina de Turing determinista) puede resolverlos en tiempo polinomial, no digamos ya la todopoderosa máquina de Turing NO determinista. Así que los problemas NP incluyen a los problemas P. La cuestión del millón de dolares es si el recíproco es cierto: ¿puede encontrarse un algoritmo rápido como el método 1 para cualquier problema NP y decir, por tanto, que todos los NP son también del tipo P?

Quizá el más famoso de los problemas NP es el del viajante de comercio. Se trata de una persona que tiene que pasar por una serie de ciudades de manera que tarde lo menos posible. Tiene el mapa con la posición de las ciudades y la distancia entre ellas. Así que una forma de resolver el problema es calcular todas las rutas posibles, ver cuántos kilómetros supone en total cada ruta y elegir finalmente la más corta. Pero, claro, ya sabemos que, si tenemos N ciudades, eso va a suponer que hay N! rutas y que eso da un tiempo no polinomial. Es el método 2 de antes. El asunto es que a día de hoy nadie ha encontrado un método 1 rápido. Ni siquiera se sabe si verdaderamente hay un método polinomial para resolverlo.

El problema del viajante de comercio tiene el interés de que es de los que se llaman NP-completo... ah...¿y eso qué quiere decir? Pues eso significa que todos los problemas NP que podamos imaginar pueden, en el fondo, transformarse en el problema del viajante. Así que, si a alguien se le ocurre un algoritmo de tipo polinomial para el problema del viajante, habrá demostrado que todos los problemas NP son en realidad problemas P, es decir, habrá demostrado que P=NP, y lo recompensarán por ello con un millón de dólares (y tal vez con la medalla Fields). O puede que no, que sea imposible encontrar un algoritmo polinomial. Si alguien demuestra que realmente es imposible, entonces habrá demostrado que P?NP y también le darán un millón de dólares (y tal vez la medalla Fields). En este último caso, podríamos olvidarnos de buscar una solución rápida al problema del viajante, porque no la habría.

Por último, para terminar de enredarlo todo un poco más, hay que tener en cuenta que hay problemas incluso más difíciles que los NP. Son problemas que ni siquiera una máquina de Turing no determinista puede afrontarlos con éxito. En fin, que no hay nada todopoderoso para las matemáticas.

18. Calculando el número ? a cañonazos

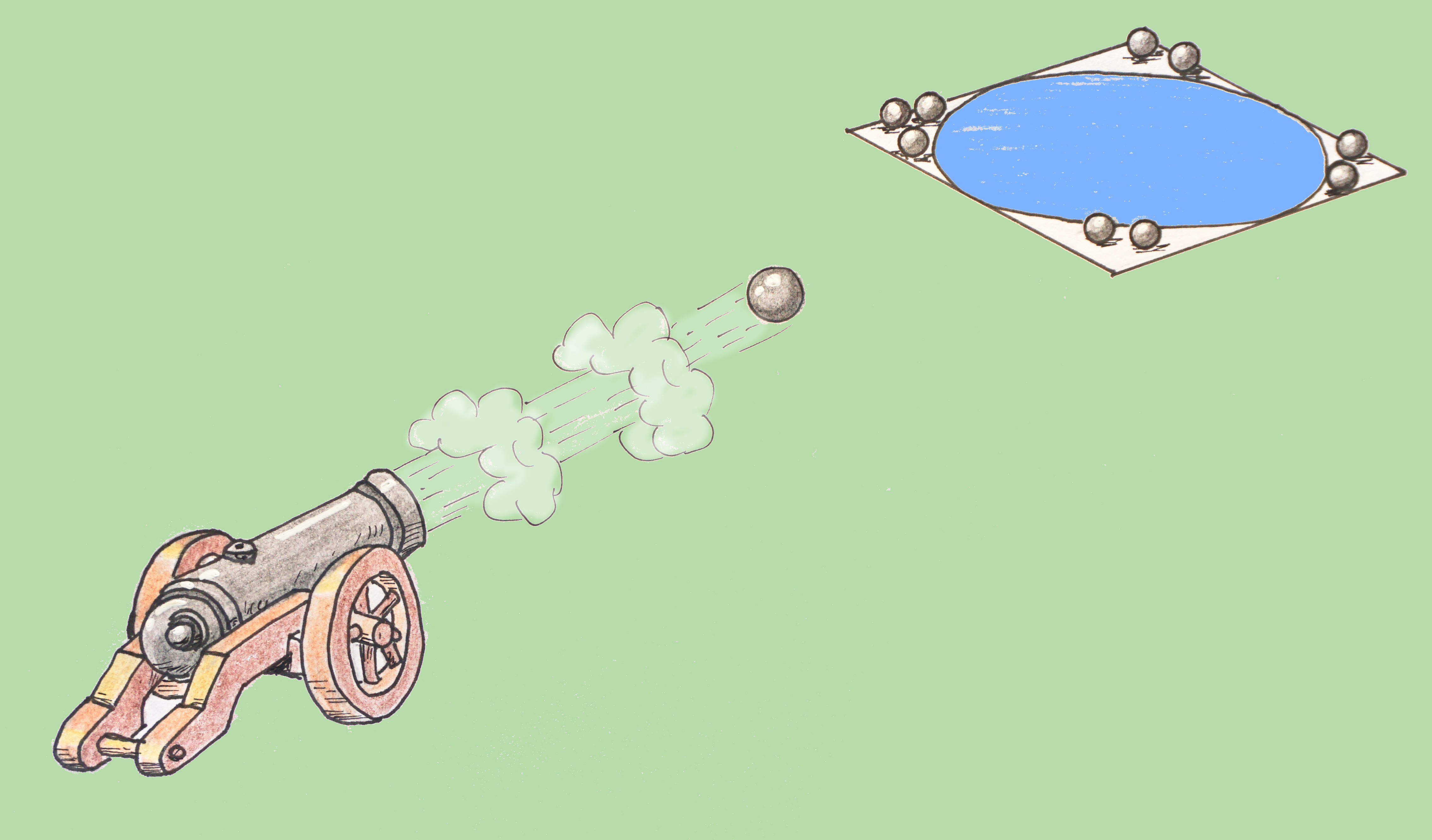
Todo el mundo sabe que el número ? tiene infinitos decimales. Por eso escribimos ? = 3,141592... con puntos suspensivos al final para indicar que siguen y siguen. Ahora bien, ¿habéis pensado alguna vez cómo podríamos calcular esos primeros decimales, o los siguientes? Hay varias formas de hacerlo, pero quizá la más rara de todas es lanzando cañonazos a un estanque. No es broma, se puede calcular a cañonazo limpio.

Imaginemos dos estanques circulares, uno más pequeño y otro más grande, con agua (en azul) situados en sendos jardines (en verde), de manera que el cuadrado total sí que sea del mismo tamaño:

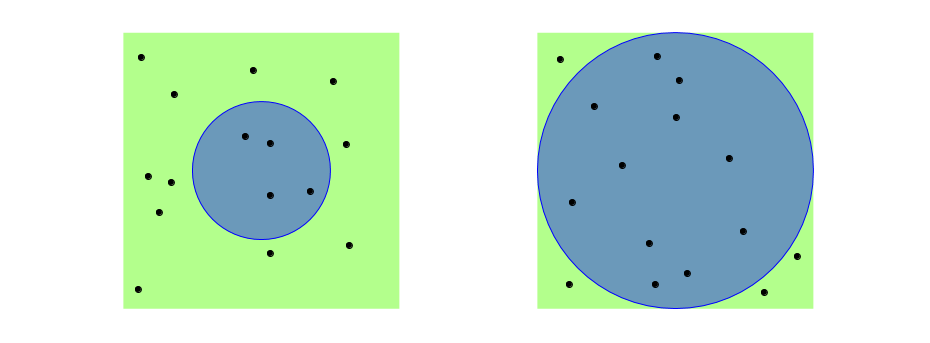
Hemos lanzado 15 cañonazos en cada uno de ellos de forma aleatoria, es decir, sin ninguna puntería. Así que los disparos (puntos negros) pueden caer al agua o no. Pero lo que está claro es que lo normal es que caigan menos al agua en el estanque de la izquierda (4 de 15) que en el de la derecha (11 de 15), pues por algo tiene más agua, ¿no? O cómo diría un matemático: el número de bolas que caen en promedio al estanque es directamente proporcional a su área. Vamos, que, cuanto más superficie tenga el círculo, más bolas caerán en él.

Pero queremos ser un poco más concretos. De todas las bolas de cañón que lanzamos, ¿qué proporción esperaríamos que cayeran al agua? Si, por ejemplo, la zona azul tiene la misma área que la zona verde, esperaríamos que la mitad cayeran al agua y la otra mitad al césped. Pero, si el agua ocupa el 20% y la zona verde el otro 80%, entonces, lo habitual es que acaben mojadas el 20%, o sea, 20 de cada 100 cañonazos que se disparen. Dicho de otra forma, el cociente entre las bolas que caen al agua y las que se lanzan en total está en proporción con el cociente entre el área de la zona azul (círculo) y el área total (cuadrado). Con esto ya tenemos una fórmula:

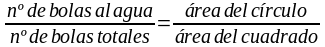
Y aquí podemos introducir ahora el deseado número ?, porque el área de un círculo de radio r es... haced memoria... ?r² y el área de un cuadrado de lado ? es... esta es más fácil... ?².

Por simplificar todo esto un poco: vamos a fijarnos solo en la figura de la derecha, la del círculo inscrito en el cuadrado. Si el círculo tiene radio r, entonces el lado del cuadrado mide el doble, o sea, 2r, y su área será ?² = (2r)² = 4r². Así la fórmula anterior se escribirá como

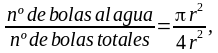
y las r se cancelan en la segunda fracción. En fin, que despejando el número ? nos queda

? = 4f,

donde por abreviar hemos llamado f al cociente ^{nº bolas al agua}/_{nº bolas totales}. Basta, pues, hacer esa división y multiplicar el resultado por 4.

A ver si sale de verdad el número ?: en nuestro ejemplo de la figura de la derecha -la fórmula hemos dicho que es para ese estanque inscrito en el jardín- tenemos que hemos colado al agua 11 de los 15 cañonazos. O sea, que el número f sería f = 11/15 = 0,73333... y al multiplicarlo por 4 nos da que ? tiene que ser 2,9333... Mmmh, ¿no tendría que dar 3,14...? Bueno, es que los lanzamientos son aleatorios y con solo 15 puede pasar cualquier cosa. Conforme tiremos más y más bolas y calculemos f con números más grandes, nos iremos poco a poco acercando al valor de ?. De hecho, harían falta miles y miles de cañonazos para empezar a estar más o menos seguros de que los primeros decimales de ? están bien calculados.

¿Y si no tenemos tantas balas de cañón? Bueno, pues en vez de cañonazos se puede hacer algo mucho más rápido y barato: simular todo esto con un ordenador. Los ordenadores son capaces de generar números (pseudo)aleatorios. También lo podéis hacer con una calculadora científica con la tecla que pone RAN#. Cada vez se genera un número decimal al azar entre 0 y 1 distinto del anterior. Si cogéis dos de ellos seguidos, podéis pensar que se trata de las coordenadas cartesianas (x,y) donde ha caído la bala de cañón. Y se pueden tirar así millones de "balas de cañón". A este tipo de simulaciones basadas en los números (pseudo)aleatorios se les llama simulaciones de Monte Carlo, y son una herramienta importantísima que se utiliza hoy en día para un montón de cosas, desde meteorología a radioterapia. Aunque, ojo, que los números esos no son aleatorios del todo y, de hecho, empieza a repetirse la serie después de unos cuantos millones de números distintos, por eso son PSEUDOaleatorios y por eso tampoco valdrían para encontrar decimales de ? indefinidamente.

De todas formas, nadie utiliza en la práctica un método de Monte Carlo para calcular decimales de ?, porque es muy lento. Incluso el antiquísimo método exhaustivo de Arquímedes, §34, tiene una convergencia más rápida. Y no digamos ya los modernos cálculos de ? basados en series como las que tan bien estudiaron Euler, §36, o Ramanujan, §7. Pero, sea como fuere, siempre es más impresionante calcular ? a cañonazo limpio, ¿verdad? Este método de los cañonazos apareció por primera vez en 1985 en la célebre revista de divulgación Scientific American, en un artículo de la sección Computer Recreations de A. K. Dewdney... aunque la idea de calcular ? lanzando cosas es mucho anterior. Ya en 1733 al conde de Buffon se le ocurrió tirar agujas sobre un suelo a rayas y preguntarse por cuántas agujas caerían justo entre dos rayas. Y sí, salía el número ? por ahí también.

19. ¿Cuánto mide un romanescu?

El romanescu es ese híbrido entre la coliflor y el brócoli de un color verde vivo, y que parece una granada extraterrestre a punto de explotar. Bien, pues la pregunta es: ¿cuánto mide? Pongamos que queremos encontrar la longitud exacta desde la parte más alta hasta su base...

Si cogemos una regla cualquiera (no hace falta que sea tan hortera como la regla rosa de la imagen), podremos tener una primera aproximación, pero seguro que mediremos de menos, porque se nos escapan las subidas y bajadas de los capullos del romanescu.

Necesitaríamos un instrumento de medida más flexible. Pues fácil: un metro de hule de esos de costura. Ahora lo vamos colocando más o menos como en la siguiente imagen (que nadie piense que la línea roja que se ve está hecha por ordenador porque es un metro de hule de verdad que tenía en el cajón junto a la regla rosa, eh)

Mucho mejor. Una medida sin duda más precisa..., pero no exacta, porque los capullos grandes del romanescu están formados a su vez por capullos más pequeños. Otra vez nos estamos quedando cortos en nuestra estimación de la longitud. Con un hilito más fino (en color azul en la siguiente ampliación) podríamos afinar otro poco, pero, si nos fijamos bien, vemos que también los capullos pequeños están formados por otros aún más diminutos, así que seguimos midiendo de menos al no tener en cuenta las mini bajadas y mini subidas. Cuanto más preciso es nuestro instrumento de medida, mayor es la longitud.

Esto de que al hacer zoom vuelva a salir la misma estructura una y otra vez es a lo que los matemáticos le dan el nombre de fractal. Estos objetos tan cansinos ya nos han salido antes al hablar del triángulo de Sierpinski, §14, o de los conjuntos de Julia, §15. Incluso definiremos en §22 una dimensión fractal que será la clave de todo.

No solo aparece esta paradoja en los romanescus (lo que podría justificarse por ser granadas de mano de origen extraterrestre, pues ya sabemos que los marcianos son muy raros), sino que incluso aquí, en la Tierra, pasan cosas así. Nuestras costas, con sus entrantes y salientes a diferentes escalas tienen algo de fractal, lo que hace que medir su longitud no sea tan fácil como podría pensarse. Ni más ni menos que Benoît Mandelbrot, el padre de los fractales, se hizo la pregunta en 1967 de cuánto mediría la costa de Gran Bretaña, una excelente excusa para hablar de la dimensión fractal. La idea venía de antes, como apunta el propio Mandelbrot, que acabó bautizando esto como el efecto Richardson en honor a Lewis F. Richardson, que ya se calentó la cabeza en los años 20 del siglo pasado con todo esto.

20. El cifrado de Vernam y el cuaderno de un solo uso del Che Guevara

Cuando en 1967 Ernesto "Che" Guevara fue capturado y ejecutado en Bolivia, llevaba -según la biografía de Daniel James- lo que se conoce como un "cuaderno de un solo uso" o "libreta de uso único" (en inglés One-Time Pad, OTP). Se trata de una libreta de claves que servía para cifrar y descifrar mensajes secretos que intercambiaba con otras personas, que debían poseer, a su vez, una copia del OTP. Precisamente, este cuaderno sirvió para descifrar una comunicación que Guevara mandó a Fidel Castro pocos meses antes de morir. La imagen siguiente muestra el proceso de codificación del mensaje del Che.

El cifrado de Vernam (1918) se basa en una clave numérica común que conocen solo el emisor y el receptor. Dicha clave permite al emisor cifrar un mensaje y al receptor descifrarlo aplicando el proceso inverso. Si la clave solo se utiliza una vez y es completamente aleatoria, se puede demostrar matemáticamente que el mensaje no puede ser descifrado por una tercera persona y entonces al cifrado de Vernam se le llama one-time pad. Ni las técnicas de criptoanálisis más modernas ni los ordenadores más potentes que podamos imaginar podrían descifrarlo. Por eso Claude Shannon, el padre de la Teoría de la Información (1948), lo definió como el "secreto perfecto". El tamaño de la clave ha de ser de al menos el tamaño del mensaje que se quiere transmitir y, como para cada mensaje nuevo hay que usar una clave distinta, lo más cómodo es tener una libreta o cuaderno de claves de donde sacar una nueva cada vez. El emisor y el receptor tienen sendos cuadernos idénticos y basta indicar al principio del mensaje, antes de cifrarlo, la página del cuaderno donde hay que mirar la clave. Los OTP fueron usados desde los años 20 del siglo pasado por los servicios de inteligencia de diversos países, especialmente por los aliados durante la II Guerra Mundial y más tarde durante la Guerra Fría por la Unión Soviética.

En la imagen de arriba de la codificación del mensaje del Che, las líneas verticales solo sirven para dividir el mensaje en columnas de cinco números en aras de la claridad. El mensaje debe leerse de izquierda a derecha teniendo en cuenta que los números están agrupados en grupos de 3 filas, como se aprecia claramente en la imagen. La primera de ellas es el mensaje sin cifrar ya convertido a números (que en principio solo conocía Guevara), la segunda es la clave (conocida por Guevara y Castro, poseedores de sendas copias del OTP) y la tercera es el mensaje cifrado que se envió (conocido por cualquiera que interceptara el mensaje, fuera amigo o enemigo).

Esta tercera fila, o sea el mensaje cifrado, se obtiene de una manera muy sencilla en el método de Vernam. Si os fijáis bien en la imagen, veréis que es simplemente la suma, dígito a dígito, de las dos filas anteriores. Así, los cinco primeros números de la imagen (mensaje sin cifrar, 06386) se transforman en 69140 porque:

0 + 6 = 6

6 + 3 = 9

3 + 8 = 11 ? 1

8 + 6 = 14 ? 4

6 + 4 = 10 ? 0

Ya veis que solo se pone la cifra de las unidades. Es lo que se llama una suma módulo 10. Cuando Castro recibía el mensaje cifrado (69140), lo único que tenía que hacer era restarle la segunda fila -que tenía en su réplica del OTP- para recuperar el mensaje original (06386). Así:

6 - 6 = 0

9 - 3 = 6

1 - 8 ? 11 - 8 = 3

4 - 6 ? 14 - 6 = 8

0 - 4 ? 10 - 4 = 6

Cuando la resta no se puede calcular con números positivos, eso quiere decir que hay que añadir una decena al minuendo, tal y como hacemos cuando restamos "con llevadas". Estamos trabajando en módulo 10.

Pero antes de eso ya hemos indicado que hay que asignar primero un código numérico a cada letra del alfabeto. Podríamos hacer A=1, B=2, C=3, D=4, E=5, F=6, G=7... hasta Z=27. Sin embargo, esta conversión plantaría un problema grave ya que, por ejemplo, el código 271 podría interpretarse como 27-1 (o sea, ZA) o bien como 2-7-1 (o sea, BGA). Para evitar eso se puede asignar a cada letra siempre dos dígitos, por ejemplo: A=11, B=12, C=13... hasta Z=37. Así ya sabemos que las cadenas de números hay que separarlas de dos en dos dígitos para pasarlas a letras. Pero la conversión a números del Che y Fidel era otra:

Leyendo la fila y la columna se saca la codificación de cada letra: A=6, B=38, C=32... Z=59. ¡Pero entonces mezclamos letras de uno y de dos dígitos de nuevo! Sí, aunque esta vez no pasa nada, porque las letras de dos dígitos empiezan siempre por 3, 5 o 7, mientras que las de 1 dígito corresponden a los número 0, 2, 4, 8, 1. No hay confusión posible. Si el mensaje con números dice 676906323997682, entonces la única separación posible es 6 76 9 0 6 32 39 9 76 8 2, es decir, la palabra ANOTACIONES, de acuerdo a la tabla de arriba. En la conversión de esa tabla se han codificado además algunos signos de puntuación y se ha reservado las codificaciones 73 y 77 para indicar el cambio de letras a números. En los mensajes de guerrilla era común que aparecieran números (heridos, municiones, dinero...). En vez de deletrearlos, era más fácil cambiar al "teclado numérico" con el código 73 y volver al "teclado alfabético" con el código 77 para seguir la frase.

¿Y por qué no es suficiente esta conversión numérica y enviar el mensaje así sin más, sin el cifrado de Vernam (lo de sumar la clave)? Pues porque, aunque a priori el enemigo no conozca la tabla de conversión entre letras y números, es relativamente sencillo sacarla mediante lo que se conoce en criptografía como un análisis de frecuencias. Basta observar qué números se repiten más y asociarlos a las letras de mayor frecuencia en el idioma del texto (en castellano las dos primeras letra son la E y la A, en ese orden). También sería fácil ir reconociendo sílabas comunes (por ejemplo EL, LA, CON, UN...). Con un ordenador moderno, en un abrir y cerrar de ojos podría romperse un mensaje de cierta extensión en el que a cada letra siempre se le asignaran los mismos números. Sin embargo, en el cifrado de Vernam una misma letra puede tomar distintos valores. Por ejemplo la palabra ANOTACIONES, que numéricamente hemos visto que es 676906323997682, se codificaría al sumarle la clave del cuaderno de uso único (en este caso es 234699362793411, como podéis encontrar en las segundas filas de la imagen de arriba si tenéis buena vista). Se obtiene así la encriptación 800595685680093, que es la serie de números que recibió Castro.

Fijaos que el primer 6 (la primera A de ANOTACIONES) se ha codificado como un 8, mientras que el segundo 6 (la segunda A de ANOTACIONES) no se ha codificado como otro 8 sino como un 0. Por eso el cifrado de Vernam es tan bueno.

Pues igual que hemos visto para la palabra ANOTACIONES, se puede ir haciendo con el resto del mensaje. En la imagen solo hay un fragmento, pero ponemos aquí completa la versión que podéis consultar en el diario del Che de Bolivia, hecho público por el gobierno cubano. El principio del mensaje que allí aparece es:

Leche: Danton llevaba un mensaje además de ANOTACIONES para memorizar el informe que le di, todo en clave. Este es el mensaje. 1°) Llegaron Danton y Francisco; este no sabía la cantidad y dejó dinero en La Paz; pienso darle 30 y reservarle el resto para cuando se alce; tiene pocas condiciones físicas y de carácter para dirigir la guerrilla, pero eso es cosa de él. Danton debe salir, pero no sé si podrá dadas las circunstancias. 2°) Se descubrió la finca y el ejército nos persiguió; le dimos la primera paliza, pero estamos aislados. 3°) Iván está listo para viajar, pero Tania está aislada aquí, pues vino violando instrucciones y fue sorprendida por los acontecimientos. 4°) Ya tenemos suficiente Glucontime, no manden más. 5°) No hay noticias del trío, tampoco confío en ellos y han expulsado a la gente de la juventud que está con nosotros. 6°) Yo recibo todo por radio, pero es inútil si no lo comunican simultáneamente a La Paz, estamos aislados por ahora. 7°) Todavía no hemos recibido mensaje a través de Lasarre. 8°) Habría que parar la carta de despedida Danton hasta nuevo aviso trataremos viaje a Francia objeto formar red de apoyo. 9°) Hice contacto Pelado objeto organizar bases al sur y colectar argentinos, también está embotellado aquí. 10°) Supriman los envíos de embutidos, pues nos tomarán maletines preparados...

Por cierto, que sigue sin ser muy comprensible, ¿verdad? Eso es porque el lenguaje contiene expresiones acordadas previamente. Por ejemplo, LECHE se refiere a Fidel Castro y DANTON a Jules Régis Debray.

Como todo lo que rodea a la muerte de Ernesto "Che" Guevara, el documento aquí transcrito no puede asegurarse veraz, y hemos de conformarnos con las referencias bibliográficas que lo citan y la aparente verosimilitud del mensaje cifrado en el contexto histórico.

21. Sándwich para dos

Imaginad un sencillo sándwich de jamón york como el de la imagen: rebanada de pan, loncha de jamón y otra rebanada de pan encima. La verdad es que, aunque pongamos una buena ración de companaje, no parece gran cosa para cenar..., pero todavía podría ser peor si además tenemos que compartirlo con alguien. O sea, que tocaríamos solo a medio sándwich (grrrr). Y claro, ante una cena tan frugal, nadie va a querer quedarse con la parte pequeña, así que habrá que coger un cuchillo y dar un corte preciso para partirlo justo justo por la mitad. Pero, ¿es eso posible?

Si el pan y el jamón estuvieran perfectamente alineados, sería muy sencillo, pues bastaría hacer el corte justo por una diagonal, o por cualquier otro plano que pasara por el centro del sándwich. Pero la realidad es que una rebanada de pan no queda exactamente sobre la otra y además el jamón suele sobresalir más por un lado que por otro. Así que ese método no nos vale, porque con tanta hambre nadie está dispuesto a conformarse con menos de la mitad, ni siquiera por unos milímetros. Y tampoco es cuestión de ponerse a separar el jamón, repartirlo a medias, luego hacer lo mismo con el pan y entonces hacer dos sándwiches. No, lo que queremos es, sin desmontar nada y con un solo corte, dividir el sándwich original en dos partes iguales. ¿Sí? Pues bien, hay una buena noticia y una mala.

Empecemos por la buena. La buena es que... ¡sí que se puede! Hay un teorema matemático, §3, que viene a decir que para tres objetos tridimensionales existe un plano que simultáneamente divide en dos partes iguales a cada uno de esos objetos. Nuestros tres objetos serían la rebanada de pan de abajo, el jamón y la rebanada de pan de arriba. De hecho, mediante ese plano -que el teorema asegura que existe-, no solo vamos a dividir en partes iguales el jamón y el pan, sino que encima las dos medias rebanadas de arriba que resulten tras el corte van a ser iguales entre sí (y lo mismo para las de abajo).

A propósito, ¿os imagináis como se llama este teorema? Exacto, el "Teorema del Sándwich de Jamón." Aunque lo cierto, es que también se podría aplicar a un bocata de lomo con queso, que es más irregular, pero que también tiene tres "objetos": pan, queso y lomo.

¿Y la mala noticia? Pues resulta que el teorema dice que existe ese plano, pero no nos dice dónde está ni tampoco nos da ninguna indicación de cómo calcularlo. Y hay que tener en cuenta que el corte (o sea, el plano) no tiene por qué ser perpendicular a las rebanadas ni siquiera pasar por el centro de cada ingrediente. Vamos, que en la práctica tendremos que conformarnos con hacer el corte a ojo y esperar que el otro comensal sea comprensivo.

22. Los fractales: otra dimensión

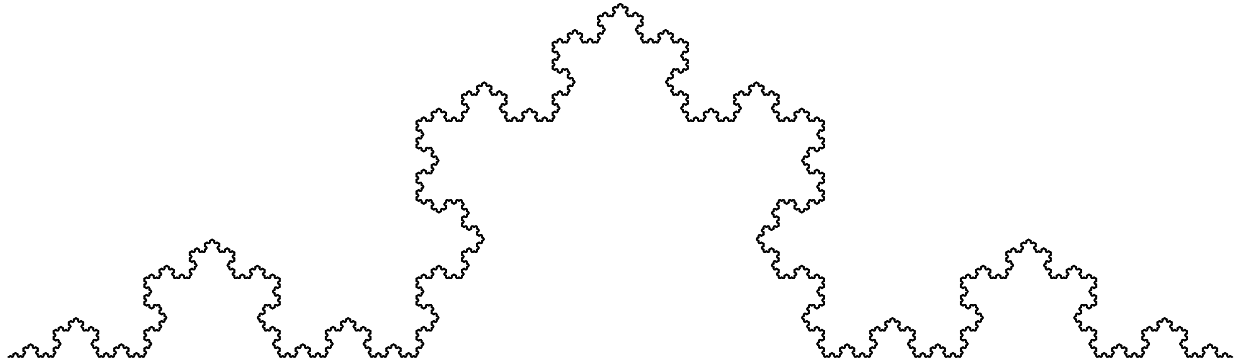
Un segmento tiene dimensión 1 (largo), un cuadrado tiene dimensión 2 (largo y ancho) y un cubo tiene dimensión 3 (largo, ancho y alto). Esta noción de dimensión es la que aprendimos en el colegio y que los matemáticos llaman dimensión topológica. Pero hay otras formas de entender la dimensión que, en cierta manera, generalizan el concepto anterior, permitiendo estudiar objetos más complicados como los fractales (ya sabéis, esas figuras que exhiben un patrón repetido a diferentes escalas y que ya vimos en §14, §15 y §19). Y el resultado, como casi todo lo que tiene que ver con los fractales, es sorprendente: ¡dimensiones con decimales!

Siguiendo los pasos de Benoît Mandelbrot -el matemático que acuño el término fractal- vamos a definir una nueva dimensión. La llamaremos dimensión fractal. En términos de proporcionalidad geométrica. Pues venga, a ver cómo queda ahora la dimensión para el segmento, el cuadrado y el cubo.

Empecemos con el segmento. Imaginemos que el segmento mide 1 metro y que lo dividimos en tres partes iguales. Cuando hacemos esto, resulta que el segmento original de 1 m contiene entonces 3 segmentos pequeños, cada uno de ellos de tamaño 1/3 de metro. Decimos que tenemos N = 3 segmentos autosemejantes (o autosimilares) tras haber aplicado un factor de escala de ε = 1/3.

Veamos ahora qué pasa con un cuadrado de lado 1 m. Como hemos hecho antes, vamos a dividir cada dirección espacial entre 3 (o sea ε = 1/3 otra vez). Así, obtendremos un cuadrado que estará formado por N = 9 cuadrados pequeños autosemejantes, ya que al haber dos direcciones espaciales tenemos 3·3 = 3² = 9 cuadraditos.

Y ahora a por el cubo de 1 m de arista. Al partir en tres trozos tanto el ancho, como el largo y el alto (o sea ε = 1/3) habremos dividido el cubo en N = 27 cubos pequeños (3·3·3 = 3³ = 27).

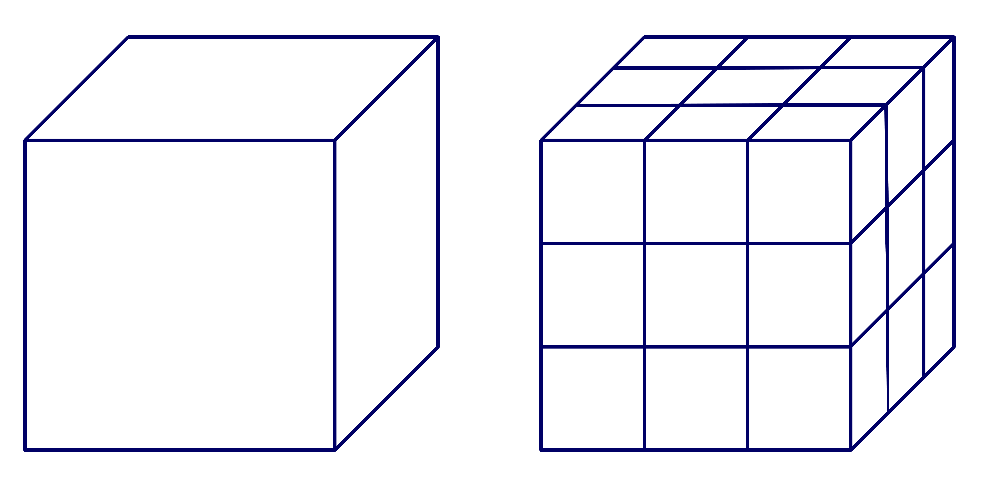
La pregunta que nos interesa es "¿qué relación hay entre N y ε para cada caso?" Lo resumimos en la siguiente tabla (daos cuenta de que ε = 1/3 quiere decir que 1/ε = 3: fracciones básicas):

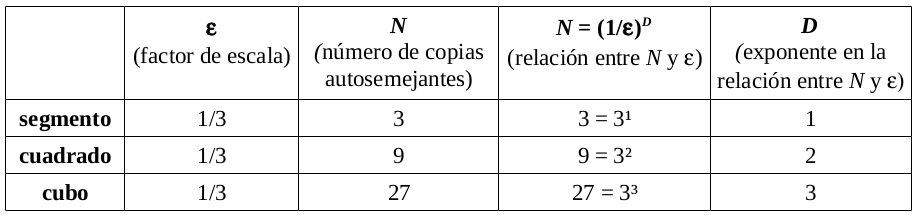
Vemos así en la última columna que el exponente D de la relación

N = (1/ε)^D

coincide con la dimensión topológica habitual. Por supuesto, podríamos haber utilizado otro factor de escala y obtendríamos el mismo exponente. Para el caso del cuadrado, por ejemplo, si el factor de escala es ε = 1/4, aparecerían N = 16 cuadrados como el original, es decir, que la relación N = (1/ε)^D sería 16 = 4² y de nuevo D = 2. Todo cuadra.

¿Y para qué tanta historia si ya habíamos aprendido en el colegio la dimensión de esos objetos de forma mucho más simple? Pues porque esta dimensión D es la que vamos a generalizar para los fractales. Lo mejor será verlo con un ejemplo concreto: la curva de Koch.

La curva de Koch se construye como sigue:

Empezamos con un segmento de 1 metro.

Lo dividimos mentalmente en 3 partes iguales (cada una medirá por lo tanto 1/3 de metro) y sustituimos el segmento del tercio central por dos segmentos (haciendo un pico como se ve en el dibujo) que midan también 1/3 de metro cada uno. Al final todos los segmentos que nos quedan miden 1/3 m, es decir, ε = 1/3.

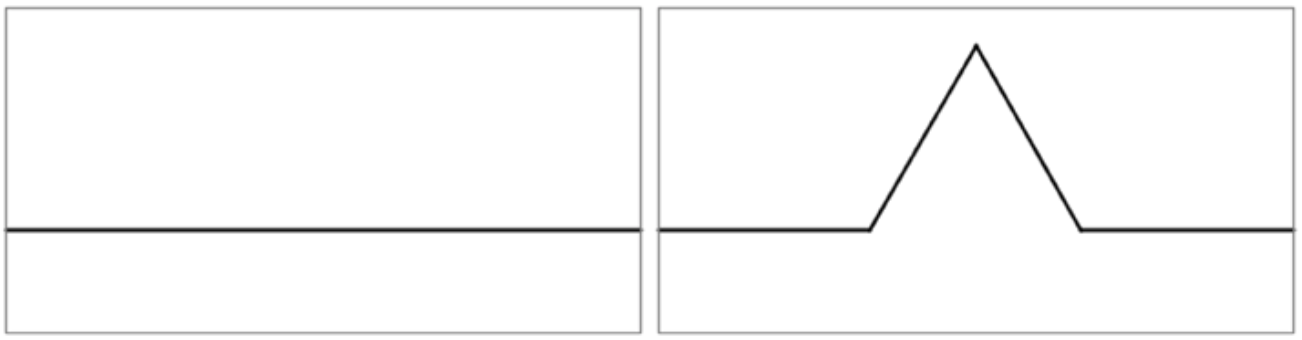
. Vamos repitiendo el paso anterior indefinidamente.

Así, en cada iteración tenemos más y más segmentos (y más y más picos), pues cada vez estamos cambiando un segmento (que podemos imaginar que está formado por 3 tercios) por 4 segmentos (cada uno de ellos de la longitud de los tercios mencionados). Evidentemente, la longitud total irá aumentando en cada iteración y podemos, por ello, decir que la curva de Koch tiene longitud infinita. Es un infinito un poco raro, porque el espacio que ocupa la curva está acotado, pero no así su longitud. En fin, cosas de fractales.

Total, que resulta que con un factor de escala ε = 1/3 obtenemos N = 4 segmentos autosemejantes cada vez. Y si nos vamos a la fórmula para la dimensión fractal D, ya sabéis, la de N = (1/ε)^D, tenemos entonces al sustituir:

4 = 3^D

Solo queda despejar la dimensión D. Está claro que D tiene que ser un número mayor que 1 (porque 3¹ = 3, que no llega a 4), pero menor que 2 (porque 3² = 9, que se pasa de 4). Así que será 1 y pico, o sea, que D es un número con decimales. ¿Y cuál es el valor exacto? Es fácil si os acordáis de los logaritmos... y si no, pues tampoco hay que agobiarse... Se despeja así:

D = log(4)/log(3)

Como todas la calculadoras científicas tienen la tecla para calcular logaritmos, es sencillísimo hacer la cuenta, que da, aproximando a las centésimas,

D = 1.26

¡Una dimensión decimal! (Bueno, la verdad es que después de avisar tanto de que iba a salir con decimales casi que sobran los signos de exclamación, ¿no?). Es como sí la curva de Koch, con sus infinitos picos, de alguna forma tuviera más dimensión que una curva unidimensional de toda la vida, y pretendiera acercarse a las dos dimensiones, pero sin llegar a conseguirlo.

Cálculos análogos pueden hacerse para encontrar la dimensión fractal de otros objetos. En general, de nuestra fórmula N = (1/ε)D podemos despejar D aplicando logaritmos para obtener:

D = log(N)/log(1/ε)

Por ejemplo, para el triángulo de Sierpinski que estudiamos en §14 sabemos que, cada vez que dividimos por 2 el lado del triángulo (esto es, ε = 1/2), obtenemos el triple de triángulos autosemejantes (esto es, N = 3). La fórmula anterior nos da entonces para la dimensión fractal D = 1.58. ¡Todavía más que la curva de Koch! E incluso, para algunos conjuntos de Julia, §15, podemos tener una dimensión fractal D = 2, es decir, son curvas unidimensionales (topológicamente hablando) tan enrevesadas que acaban de alguna forma comportándose como objetos bidimensionales que rellenan el plano completamente.

Y para acabar haciendo honor a los fractales, volvamos al primer párrafo. Allí dijimos que "hay otras formas de entender la dimensión". Sí, dijimos eso, formas. En plural. O sea, que hay varias maneras de definir la dimensión fractal, aunque no creo que a estas alturas nadie quiera enredarse con los detalles de las dimensiones de Hausdorff-Besikovitch o de Minkowski-Bouligand...

23. El número de Dios del demoniaco cubo de Rubik

El cubo de Rubik es ese juguetito que triunfó en la década de los 80 del siglo pasado, y que consiste en romperse la cabeza hasta conseguir que cada una de las 6 caras de un hexaedro (o sea, un cubo) esté formada por 9 cuadraditos del mismo color. Una cara puede girar independientemente de las otras gracias a un mecanismo de ejes. Cada movimiento de las caras del cubo de Rubik hace que se vayan cambiando las posiciones de los colores de los cuadrados. Es un invento del maligno, nadie lo duda. Pero aquí no vamos a hablar de demonios, sino de dioses, en concreto del "número de Dios" o, lo que es igual, el número mínimo de movimientos que son suficientes para resolver un cubo de Rubik por muy desordenado que esté.

Pero antes de deciros cuál es el número de Dios vamos a definir bien todo. En las clases del instituto de finales del siglo XX se explicaba en detalle el concepto matemático de "grupo". Sin embargo, ahora todo eso de los grupos ya no está tan de moda, así que mejor lo repasamos...

Un grupo es una estructura matemática muy general formada por dos ingredientes: un conjunto y una operación entre los elementos del conjunto. Esa operación coge dos elementos del conjunto y al operarlos saca otro elemento también del conjunto, de forma que se cumplen las siguientes condiciones:

1. En el conjunto hay un elemento (llamado elemento neutro) con la propiedad de que, al operar un elemento cualquiera por el elemento neutro, se obtiene el mismo elemento. Es decir, que operar con el elemento neutro es como no hacer nada.
   
2. Para cada elemento del grupo existe otro elemento (llamado su inverso), de suerte que al operarlos juntos se obtiene el elemento neutro.
   
3. La operación es asociativa. Esto quiere decir que, si tenemos tres elementos del conjunto y operamos el primero con el segundo y luego lo que nos dé lo operamos con el tercero, vamos a obtener el mismo elemento que si operamos el primero con el resultado de la operación del segundo con el tercero.
   

Ya está, esto es un grupo: una pareja de conjunto y operación con las propiedades anteriores. Más claro se verá con un ejemplo. El conjunto de los números enteros con la operación suma tiene estructura de grupo. En efecto, se cumplen las tres condiciones:

1. El elemento neutro es el número 0. Para cada número a tenemos que a+0=a. También hay que comprobar que se cumple al revés: 0+a=a, porque en la definición de grupo no se presupone la propiedad conmutativa (por cierto, que los grupos que son además conmutativos se llaman grupos abelianos en honor de Abel, del que hablamos al final de §13).
   
2. Si a cada número le sumamos su opuesto (el mismo número pero cambiado de signo), nos da 0, que era precisamente el elemento neutro. Por ejemplo, 7+(?7) = 0. Diríamos que ?7 es el inverso de 7.
   
3. Se cumple la propiedad asociativa. Por ejemplo, (1+2)+3 = 1+(2+3). La cuenta da 6 la hagas con un orden o con otro.
   

Hasta aquí parece un poco aburrido; lo verdaderamente interesante de los grupos es su generalidad. Y es que los conjuntos no tienen por qué estar formados por números y la operación no tiene por qué ser una suma o una multiplicación, lo que nos va a permitir definir una estructura de grupo en el cubo de Rubik. Ahora el conjunto va a tener como elementos los distintos movimientos que podemos hacer y la operación va a ser simplemente la concatenación de dos movimientos, uno tras otro. Normalmente se utiliza la siguiente nomenclatura. U (up), F (front), D (down), B (back), R (right), y L (left) representan un giro de 90° en el sentido de las agujas del reloj de las caras superior, frontal, de abajo, de atrás, derecha e izquierda, respectivamente. Con un superíndice 2 se representan los giros de 180° en sentido horario (por ejemplo U2 es un giro de 180° en sentido horario de la cara superior) y con una prima se representan los giros de 90° en sentido antihorario (por ejemplo L' es un giro de ?90° de la cara izquierda del cubo). Además, añadiremos el "movimiento" que consiste en no hacer nada. Con estos ingredientes puede comprobarse que tenemos una estructura de grupo.

Varias letras seguidas indican el movimiento resultante de la concatenación de los movimientos elementales que acabamos de definir. Por ejemplo, U'R es el movimiento global que resulta de primero girar ?90° la cara superior y luego girar 90° la cara de la derecha. Hemos operado (concatenado) dos movimientos para obtener un tercero. O por ejemplo, U2U equivale a U'. Incluso podemos considerar movimientos más largos como, por ejemplo, U'RU2LDL. Todos estos son ejemplos de elementos del grupo del cubo de Rubik. Puede verse que el número total de movimientos distintos que podemos hacer en el cubo (o sea, el número de elementos de nuestro conjunto) se corresponde con el número distinto de configuraciones de color del cubo de Rubik. Aunque el grupo no tiene infinitos elementos (como sí ocurría en el grupo de los números enteros con la suma), no cabe duda de que hay un montón de movimientos posibles. En concreto, la cardinalidad (ese es el tecnicismo para hablar del número de elementos) del grupo del cubo de Rubik es 43 252 003 274 489 856 000.

En teoría de grupos hay muchísimos teoremas que podemos aplicar al cubo de Rubik para entender mejor cómo resolverlo..., pero nosotros nos bajamos aquí. Por lo menos ya sabemos el abc de esta rama abstracta de las matemáticas. Que quede claro, además, que aunque no esté muy de moda, como decíamos antes, la teoría de grupos es fundamental en distintos campos científicos como, por ejemplo, la mecánica cuántica o la física del estado sólido.

Ah, espera, se me olvidaba lo del número de Dios. Es 20. Las posiciones más difíciles del cubo de Rubik se pueden ordenar tras concatenar 20 movimientos elementales del tipo U, U2, U', F, F2... No hacen falta más giros de caras si uno elige los movimientos precisos (en el orden también preciso porque el grupo no es abeliano), entendiendo que cada giro de una cara puede ser de 90° -sentido horario o antihorario- o de 180°. (Si, por contra, se considera el convenio de que los giros de 180° cuentan como dos movimientos, entonces el número de Dios es 26.)

En 1981 ya se demostró que el número de Dios debía estar entre 18 y 52. En 1995 se encontró que algunas posiciones necesitaban al menos 20 movimientos, por lo que el número de Dios debía ser mayor o igual a 20. La demostración de que era exactamente 20 tuvo que esperar hasta el año 2010, tras tres décadas de sucesivas mejoras en las acotaciones del número de Dios. Como con el famoso Teorema de los Cuatro Colores, §6, se han necesitado potentes ordenadores para realizar cálculos, una vez que los casos interesantes se han reducido a unos pocos mediante razonamientos matemáticos de teoría de grupos.

Aún quedan muchos interrogantes sobre el cubo de Rubik, como por ejemplo cuál es el algoritmo óptimo (el que usa menos pasos) para una cierta configuración de partida general. Porque ya tenemos clarísimo que el que el número de Dios sea 20 no quiere decir que haga falta gastar siempre los 20 movimientos. De hecho, solo hay alrededor del 0.000001% de las posiciones del cubo de Rubik que requieren exactamente los 20 movimientos. ¿Más cuestiones abiertas? Pues resulta que todo esto es para el cubo original de tamaño 3×3×3, pero también hay cubos más grandes (por ejemplo 4×4×4). Y para estos no se conoce todavía su número de Dios.

24. Una nueva geometría rara: de Euclides a Riemann

Los tres ángulos de un triángulo suman 180º. Dos rectas paralelas son siempre equidistantes. ¿Son estas archiconocidas afirmaciones geométricas realmente verdaderas? Bueno, pues la respuesta no es nada evidente. Hasta el punto de que hicieron falta más de dos mil años para que alguien consiguiera explicarlo bien. Y después de tanto tiempo dándole vueltas a la pregunta y de tantos esfuerzos vanos, resultó que de repente casi a la misma vez tres matemáticos (un ruso, un húngaro y un alemán) dieron con la clave de manera independiente.

Empecemos por el principio, o sea, por Euclides, §11. Su libro los Elementos parte de algunas definiciones básicas y de cinco postulados. Estos últimos son verdades evidentes que hacen que toda la geometría propuesta por él sea consistente y permiten construir sobre ellos el resto de resultados. No son proposiciones o teoremas que hayan de ser demostrados (como explicamos en §3), sino que son afirmaciones tan simples y lógicas que no pueden ser de otra forma. En un lenguaje moderno, los cinco postulados que escribió Euclides vienen a decir lo siguiente:

• Postulado I: Se puede trazar una línea recta de un punto cualquiera a otro punto cualquiera.
• Postulado II: Un segmento se puede extender indefinidamente en una línea recta.
• Postulado III: Se puede trazar una circunferencia con cualquier centro y radio.
• Postulado IV: Todos los ángulos rectos son iguales entre sí.
• Postulado V: Si una línea recta corta a otras dos, de tal manera que la suma de los dos ángulos interiores del mismo lado sea menor que dos ángulos rectos, las otras dos rectas se cortan, al prolongarlas, por el lado en el que están los ángulos menores que dos rectos.

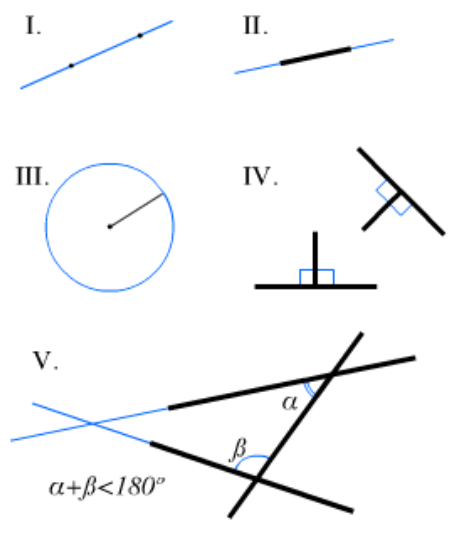
Hay algo raro aquí, ¿verdad? Mientras que los cuatro primeros postulados son verdades de Perogrullo, el postulado V es mucho más largo y menos claro. Parece más bien un teorema que pudiera ser demostrado a partir de los cuatro postulados previos. De hecho, así lo creyeron muchos matemáticos que durante casi veintidós siglos fracasaron en encontrar una prueba del quinto postulado. Eso sí, por el camino fueron apareciendo multitud de formulaciones equivalentes y algo más breves, como por ejemplo:

Por un punto exterior a una recta dada se puede trazar una única recta paralela.

A esta formulación se la conoce también como axioma de Playfair (finales s. XVIII). Es una de las formas equivalentes más comunes de enunciar el quinto postulado de Euclides, que también se llama por ello el "postulado de las paralelas".

O esta otra tan famosa:

La suma de los ángulos de un triángulo es de dos ángulos rectos (180º).

La equivalencia entre esta afirmación (bien conocida ya hacia el s. IV a. C.) y el quinto postulado de Euclides se debe al matemático francés Legendre (s. XIX).

Por cierto, ¿os acordáis de la "demostración" que nos enseñaban en la escuela para ver esto de que los ángulos de un triángulo suman 180º? Para empezar se trazaba una paralela a uno de los lados del triángulo por el vértice opuesto y... es decir, ¡que se usaba en el fondo el quinto postulado!

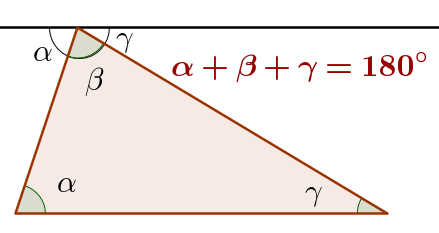
Así es como lo demuestra el propio Euclides en la proposición número 32 del primer libro de los Elementos. No tiene más remedio que usar su quinto postulado, algo que sí que consiguió evitar en sus primeras 28 proposiciones. Probablemente, Euclides ya veía algo raro en el último postulado y trataba de dejarlo de lado para demostrar sus teoremas en la medida de lo posible.

Pero vamos ya a los tres matemáticos (el ruso, el húngaro y el alemán):

. El ruso: Nikolai Lobachevski. En un trabajo publicado en 1829, propuso una nueva geometría en la que no se prohibía que por un punto exterior a una recta pudieran trazarse dos o más rectas paralelas a la primera (es decir, dos rectas distintas tales que ninguna de ellas se cruzara con la primera recta). En otras palabras, Lobachevski se preguntó qué ocurriría al postular lo contrario al axioma de Playfair. Y lo que obtuvo fue una geometría no euclidiana sin ninguna contradicción lógica, tan válida como la de Euclides, aunque difícilmente imaginable. Pero precisamente el paso de lo palpable a lo abstracto es la clave de la matemática moderna. Partiendo de los cuatro primeros postulados de Euclides y de la afirmación opuesta al quinto postulado, podían obtenerse teoremas en los que todo cuadraba. Las cosas cambiaban ahora, claro. Por ejemplo, la suma de los ángulos de los nuevos triángulos "imaginarios" de Lobachevski tenía que ser menor de 180º. Cómo dibujarlos era otra cosa ya...

. El húngaro: János Bolyai. Su padre, el también matemático Farkas Bolyai, había pasado años y años intentando infructuosamente probar el quinto postulado de Euclides, y no dudó en tratar de disuadir a su hijo János de que siguiera sus pasos: un camino que podría acabar obsesionándolo a costa de la salud, la cordura y la felicidad. Pero János perseveró y acabó llegando a las mismas conclusiones que Lobachevski. Los resultados de János Bolyai, fechados también en 1829, no fueron publicados, sin embargo, hasta tres años después, en un anexo a un tratado de su padre. En cualquier caso, no queda duda de que János Bolyai llegó a las mismas conclusiones que Lobachevski de manera independiente, entre otras cosas porque este último había escrito sus trabajos en ruso, y no fueron conocidos en Europa occidental hasta años más tarde.

. El alemán: Carl Friedrich Gauss. Apodado el Príncipe de los matemáticos, es unánimemente reconocido como uno de los más grandes matemáticos de todos los tiempos, junto con Arquímedes, §34, y Newton, §2. En el año 1829 (otra vez el mismo año, sí), Gauss expone a un colega en una carta privada que había hecho extensas investigaciones sobre una geometría sin el quinto postulado de Euclides, pero que no se atrevía a publicarlas por la enorme controversia que esta nueva geometría podría suponer en la comunidad matemática. No olvidemos que en esa época Gauss gozaba ya de un reconocimiento importante y se encontraba en una situación cómoda. Así que, cuando Farkas Bolyai envía una copia con los resultados de su hijo a su colega y amigo Gauss, éste le contesta que:

Si empiezo diciendo que no puedo alabar semejante trabajo te sentirás desconcertado, pero no puedo hacer otra cosa, porque alabarlo sería alabarme a mí mismo, pues todo el contenido del escrito, el camino seguido por tu hijo y los resultados a los que ha llegado coinciden casi completamente con mis meditaciones, parte de las cuales han tenido lugar desde hace 30 o 35 años.

En cualquier caso, Gauss no dudó después en reconocer públicamente la originalidad y genialidad de las publicaciones de János Bolyai (que conoció en 1832) y de Lobachevski (que conoció en 1841).

Si la geometría de Euclides correspondía a triángulos cuyos ángulos sumaban exactamente 180º, la nueva geometría de Gauss/Bolyai/Lobachevski (conocida como geometría hiperbólica) corresponde a triángulos cuyos ángulos suman menos de 180º. El caso restante, a saber, triángulos con más de 180º, daba una geometría con contradicciones lógicas y por tanto no válida, por lo que Gauss, Bolyai y Lobachevski la desecharon desde el principio.

Pero algunos años más tarde, Bernhard Riemann -el de la complicadísima hipótesis de Riemann que intentamos explicar en §8- dio otro paso. Si, además del quinto postulado de Euclides, eliminamos también el segundo postulado, entonces sí que podemos tener una geometría cuyos triángulos tengan ángulos que sumen más de 180º y que sea consistente desde un punto de vista lógico. En este segundo tipo de geometría no euclidiana, llamada geometría elíptica, podemos decir que las líneas rectas son como círculos, de manera que tienen una longitud finita, pero a su vez no tienen fin. Y, a diferencia de la geometría hiperbólica, esta sí que es fácil de imaginar, porque es la que se encuentra, por ejemplo, en una superficie esférica. Basta pensar en el triángulo que se formaría sobre la superficie de nuestro planeta a partir de dos meridianos y un paralelo. Dos de sus ángulos serían rectos y todavía habría que sumarles un tercero (el del polo), con lo que su suma sería siempre mayor de 180º.

Así que para cerrar habría que añadir a Riemann con su geometría elíptica como pionero -junto con Bolyai, Lobachevski y Gauss con la geometría hiperbólica- de las llamadas geometrías no euclidianas, que podemos decir que son geometrías curvas, en contraposición a la geometría plana euclídea. Pero, ojo, que desde un punto de vista de la lógica matemática son tan buenas unas como otras.

25. La frecuencia de la música

Si acercamos la cara a unos altavoces a todo volumen, notaremos el aire que sale e incluso veremos la membrana del altavoz vibrar. Estas vibraciones de la membrana hacen que las moléculas de aire sean golpeadas y salgan propulsadas una y otra vez formando una onda de presión que percibimos como sonido cuando es registrada por nuestro oído.

Una nota musical es una de estas ondas acústicas. Cada nota se caracteriza por la frecuencia que tiene, es decir, por cuántas veces por segundo se repite el movimiento de las moléculas adelante y atrás. La frecuencia se mide en hertzios (abreviado Hz). El número de hertzios es simplemente el número de veces que se repiten los "golpes" de la onda por segundo.

El oído humano puede captar desde sonidos muy graves de unos pocos hertzios hasta muy agudos de miles de hertzios. A una onda cuya frecuencia es de exactamente 440 Hz es a lo que en música se le llama nota LA. Cualquier onda que tenga una frecuencia que sea un múltiplo de ese valor de 440 Hz (880 Hz, 1320 Hz, 1760 Hz...) o un submúltiplo (220 Hz, 110 Hz, 55 Hz...) será también la nota LA: sonará más agudo o más grave que nuestro LA de partida, pero conservará su sonido característico de LA.

¿Y qué ocurre con las frecuencias intermedias entre dos de estos LA consecutivos, digamos por ejemplo entre el LA de 440 Hz y el siguiente LA más agudo de 880 Hz? Es sencillo: entre ellos se encuentran el resto de notas musicales, que también tienen sus frecuencias típicas. Al intervalo entre dos notas LA consecutivas (o entre otras dos notas iguales en su sonoridad) se le llama en música una "octava".

Una vez fijado el LA de 440 Hz podemos encontrar las frecuencias de las otras notas. Pero antes de ponernos manos a la obra, hay que tener claro cuántas notas hay. ¿Lo sabéis?... ¿seguro?... Hay 12 notas musicales. A ver, vamos a contar. DO, RE, MI, FA, SOL, LA, SI... Eso son 7, ¿y las que faltan hasta 12? Pues se llaman DO#, RE#, FA#, SOL# y LA# (el símbolo # se lee "sostenido") . A los músicos les gusta mucho esta forma de nombrar las 12 notas, pero desde el punto de vista de sus frecuencias la onda del DO# no tiene nada de especial; ni siquiera tiene más relación con el DO que la relación que hay entre el FA y el MI. Un físico o un matemático etiquetarían las notas con un número n del 1 al 12 en lugar de utilizar esos nombres. Las 12 notas ordenadas de grave a agudo (o sea, de menor a mayor frecuencia) quedarían así:

A lo que íbamos, queremos encontrar las frecuencias de las notas comprendidas entre el LA de 440 Hz y el de 880 Hz. Una primera idea (errónea) sería dividir el intervalo de frecuencias en 12 partes iguales y a cada una de las frecuencias que nos dan el cambio de intervalo le llamaríamos LA#, SI, DO, DO#, RE... (o en lenguaje matemático n = 2, 3, 4, 5, 6...), pero esa aproximación no sería útil. No queremos que la distancia entre dos notas consecutivas sea el mismo número de hertzios. Entre otros problemas, eso haría que en la siguiente octava las notas no fueran el doble que sus homónimas. Lo que queremos es que el porcentaje que incrementamos la frecuencia de una nota a la siguiente sea siempre el mismo. Es equivalente a decir que la frecuencia de cada nota se obtiene multiplicando la frecuencia de la anterior por un cierto número que vamos a llamar r. Si designamos por f_n la frecuencia de la nota n, tenemos que f₁ sería la frecuencia de nuestro LA de partida (o sea, f₁ = 440 Hz) y f₁₃ sería el LA de la siguiente octava (o sea, f₁₃ = 880 Hz). Podemos decir entonces que f₁₃ = 2·f₁.

En general,

f_n+12 = 2·f_n

Además, como cada nota se obtiene multiplicando la inmediatamente anterior por r, tendremos

f_n = r·f_n-1

Para no liarnos tanto, vamos a volver a nuestras notas con números. A ver si queda claro lo siguiente:

f₁₃ = r·f₁₂ = r·r·f₁₁ = r·r·r·f₁₀ = r⁴·f₉ = r⁵·f₈ = ... = r¹²·f₁

¿Se entiende? Y como también dijimos que esa f₁₃ tiene que ser justo el doble que f₁, pues no queda otra que r¹² = 2, con lo que, despejando,

Hablando en tanto por ciento diríamos que cada nota tiene una frecuencia que es el 105,9% de la anterior, o, más claro aún, cada nota aumenta un 5,9% la frecuencia de la anterior.

Ahora ya podemos calcular la frecuencia correspondiente a cualquier nota, pues tenemos un problema matemático perfectamente definido. Si estuviéramos en 3° de la ESO, la profesora de matemáticas diría: "hallar el término general de la progresión geométrica cuyo primer término es 440 y cuya razón es "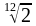

Y el estudiante plantearía el problema como

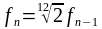
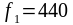
Y sabría entonces que el término general es 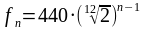. O bien, poniendo la raíz en forma exponencial:

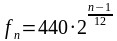
Sustituyendo en esta fórmula la letra n por los valores enteros del 1 al 12, obtenemos la frecuencia de las 12 notas musicales con las que se construye toda la música occidental. Ni que decir tiene que las otras octavas son múltiplos y submúltiplos de estas, tal y como se refleja también en la fórmula. Mostramos los resultados a continuación con las frecuencias redondeadas al número entero más próximo.

Todo esto no tiene solo interés teórico, sino que además tiene aplicación práctica. Y no solo para la música electrónica (donde es evidente). Cuando un luthier va a fabricar una guitarra, debe colocar los trastes (las tiras metálicas que hay sobre el mástil) en las posiciones adecuadas para que suenen las notas correctas. Al pisar con el dedo sobre el mástil, lo que estamos haciendo es disminuir la longitud de la cuerda y, en consecuencia, aumentar su frecuencia.

La quinta cuerda de la guitarra (contada desde abajo) se suele afinar en LA. Si "pisamos" con el dedo el mástil de forma que la cuerda toque el primer traste, la nota de esa quinta cuerda deberá ser un LA#. En el segundo traste será un SI, en el tercero un DO, en el cuarto un DO#... Por ello, si L es la longitud de la cuerda, entonces el luthier colocará el traste número n a una distancia d_n medida desde el puente que vendrá dada por la siguiente fórmula:

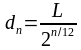
¿Véis por qué?