La relación entre arte y arquitectura es una constante a lo largo de la historia de la humanidad, desde el empleo de la geometría en la construcción, pasando por la proporción áurea hasta nuestros días.
Sin embargo, se tiende a pensar en la historia de la arquitectura como un desarrollo progresivo de diferentes estilos, donde existen unos periodos de esplendor y de armonía reinados por las leyes de las matemáticas y la pureza (como el renacimiento) que más tarde desembocan en el exceso y desequilibrio de una degeneración (como el barroco) hasta una restitución de este y la vuelta al equilibrio (neoclasicismo) hasta una nueva perturbación (romanticismo).
Esta visión puede desembocar en una falta de interés (desde el punto de vista de las matemáticas) por estos estilos considerados como caóticos o desequilibrados; pero por suerte, las matemáticas de la actualidad están dotadas de novedosas aportaciones que le permiten analizar elementos hasta ahora insospechados.
Una de estas nuevas aportaciones es la denominada geometría fractal, que tiene su origen en buscar una explicación a las curvas no diferenciables y que terminó por configurar una geometría de los denominados fractales. En realidad, un fractal es: “por definición, un conjunto cuya dimensión de Hausdorff-Besicovitch es estrictamente mayor que su dimensión topológica” 1(D > DT) (D > DT) que en un lenguaje más liviano se refiere a toda aquella figura cuya dimensión fractal (concepto aclarado a continuación) es estrictamente mayor que su dimensión topológica (bastará con entender esta noción como la dimensión ordinaria de un elemento; 1 para una curva, 2 para una superficie y 3 para un volumen).
El término dimensión fractal hace referencia a una magnitud resultado de lo que podríamos llamar la ecuación fundamental de la geometría fractal. Esta ecuación fue elaborada por el matemático Benoît Mandelbrot2, y está basada tanto en estudios empíricos3 como en trabajos de anteriores matemáticos. Su expresión resulta la siguiente:
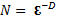
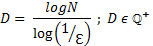
Donde N es el número de fragmentos en que dividimos el elemento, ε es la longitud de cada uno de estos fragmentos y D es la dimensión fractal (que puede tomar valores fraccionarios). Veamos que se cumple para una recta (dimensión 1):
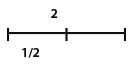
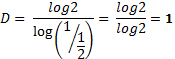
En el caso anterior, la dimensión fractal coincide con la dimensión topológica (1=1), así que veamos cómo se comporta una curva de lo más atópica: La curva de Koch:
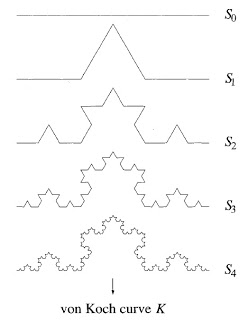
Esta curva, formada por infinitas iteraciones, añade 4 nuevas partes de tamaño 1/3 a cada nueva interacción, de manera que podemos calcular:
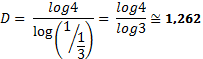
Mientras que, al ser una curva, su dimensión topológica sigue siendo 1, de manera que se cumple la proposición D > DTD > DT, (1,262 > >1) tratándose en efecto de un fractal. Este fractal en concreto, al igual que otros como el triángulo de Sierpinski, tiene además la propiedad de ser autosemejante (si ampliamos cualquiera de las partes se obtiene de nuevo toda la figura).
Está claro que los fractales comentados corresponden a curvas teóricas, producto de la imaginación de los matemáticos, pero, ¿podremos encontrar algún atisbo de esta clase de figuras (autosemejantes) en algún estilo arquitectónico de la Catedral de Murcia? Para ello analizaré los perfiles de los arcos y nervaduras de la Catedral. Esto es debido a que son uno de los elementos arquitectónicos de mayor importancia, además de un reflejo de la estética de cada época.

Figuras 1 y 2. Esquema que presenta los perfiles de nervaduras y arcos de la Catedral. El plano que acompaña nos indica en qué lugar está ubicada cada nervadura y por tanto a qué periodo pertenece. Ver Boti, Alfredo Vera. 1994. La Catedral de Murcia y su plan director. Murcia : Colegio Oficial de Arquitectos de Murcia, 1994.
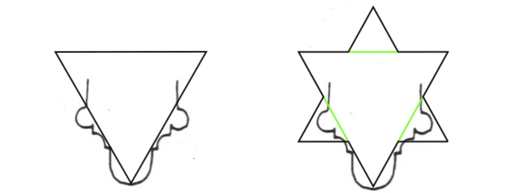
En la figura 2 se muestra la semejanza con el copo de nieve de Koch (curva de Koch para un triángulo) de la nervadura F1. Elaboración propia.
A primera vista se aprecia una cierta similitud con las figuras y la curva de Koch. Para corroborarlo utilizaré el programa informático ImageJ que me permite calcular la dimensión fractal de las imágenes mediante el método de Box-Counting4. Una vez realizados los cálculos resulta la siguiente tabla:
| Nº | Nervadura | Semejanza | Periodo |
|---|---|---|---|
| 1 | C4 | 99,842 | Gótico 2 |
| 2 | C2 | 99,527 | Gótico 3 |
| 3 | F4 | 99,527 | Gótico 1 |
| 4 | E7 | 99,525 | Gótico 1 |
| 5 | A10 | 99,448 | Barroco 2 |
| 6 | F2 | 99,214 | Gótico 4 |
| 7 | A3 | 99,128 | Gótico 3 |
| 8 | B2 | 99,058 | Gótico 2 |
| 9 | A5 | 98,980 | Gótico 2 |
| 10 | E4 | 98,825 | Gótico 1 |
| 11 | F5 | 98,825 | Gótico 1 |
| 12 | F1 | 98,732 | Gótico 4 |
| 13 | B1 | 98,671 | Gótico 3 |
| 14 | A8 | 98,671 | Barroco 2 |
| 15 | A12 | 98,653 | Barroco 2 |
| 16 | E5 | 98,440 | Gótico 1 |
| 17 | B3 | 98,363 | Renacimiento |
| 18 | E6 | 98,210 | Gótico 1 |
| 19 | F6 | 98,210 | Gótico 1 |
| 20 | A9 | 98,019 | Barroco 2 |
| 21 | C1 | 97,981 | Gótico 3 |
| 22 | A11 | 97,940 | Barroco 2 |
| 23 | B4 | 97,905 | Gótico 2 |
| 24 | D2 | 97,781 | Gótico 3 |
| 25 | C6 | 97,754 | Renacimiento |
| 26 | A2 | 97,678 | Gótico 3 |
| 27 | E1 | 97,623 | Gótico 1 |
| 28 | A1 | 97,544 | Renacimiento |
| 29 | B5 | 97,527 | Gótico 4 |
| 30 | C5 | 97,452 | Barroco 2 |
| 31 | E2 | 97,227 | Gótico 1 |
| 32 | E3 | 97,152 | Gótico 1 |
| 33 | A4 | 97,152 | Gótico 2 |
| 34 | C7 | 97,152 | Renacimiento |
| 35 | F3 | 97,002 | Gótico 1 |
| 36 | D1 | 96,434 | Gótico 3 |
| 37 | D4 | 96,434 | Gótico 2 |
| 38 | B6 | 96,336 | Renacimiento |
| 39 | C3 | 95,897 | Gótico 2 |
| 40 | A7 | 95,389 | Neoclásico |
| 41 | A6 | 95,173 | Renacimiento |
| 42 | C8 | 94,390 | Renacimiento |
| 43 | D3 | 92,314 | Renacimiento |
Tabla 1. Figuras ordenadas conforme a la mayor semejanza con la curva de Koch (D=1,262). Elaboración propia.
La tabla nos muestra cómo los arcos y nervaduras que presentan mayor semejanza con el fractal de la curva de Koch son las pertenecientes al periodo gótico y barroco, mientras que quien obtiene los peores resultados es el renacimiento, seguido del estilo neoclásico.
La principal conclusión que deriva de este hecho es la noción, aunque primitiva, de formas autosemejantes en el gótico:
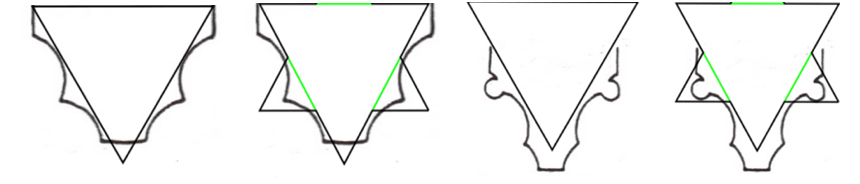
Figura 3. Superposición de la curva de Koch a las nervaduras que han obtenido mejor resultado (C4 y C2) ambas del periodo gótico. Elaboración propia.
Pero, ¿bastan estos datos para sacar conclusiones? Indagando en la ornamentación gótica se descubren otros ejemplos de fractales autosemejantes primitivos como los anteriormente descritos:
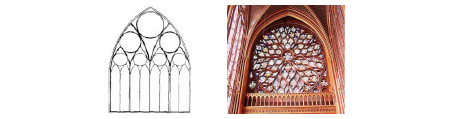
Figuras 4 y 5. Vidriera de la catedral de Metz y detalle de la Santa Capilla francesa. Ambas del periodo gótico. Se aprecia el carácter de autosemejanza de las figuras.
De manera que podemos llegar a la conclusión de que, a través del análisis fractal de la catedral de Murcia y de los perfiles de arcos y nervaduras que la constituyen se han obtenido unos datos que revelan cómo las nervaduras del periodo gótico son las más semejantes a un fractal, concretamente a la curva de Koch. Este hecho, junto con el análisis de otros elementos de ornamentación gótica (figuras 4 y 5) revelan que en la estética de este periodo se manifiesta una idea y noción primitiva de autosemejanza.
No se trata, por tanto, de un desorden, si no de otro orden distinto; lo que antes era caótico, ahora alberga una armonía que es posible desentrañar gracias a la geometría fractal, y que vuelve a hacer hincapié en el profundo vínculo entre la belleza y las matemáticas.
1 Benoît Mandelbrot. 2009. La Geometría Fractal de la Naturaleza. [trad.] Josep Llosa. 3º Edición. Barcelona: Tusquets, 2009.
2 Matemático polaco conocido por el desarrollo de la geometría fractal.
3 Por motivos de extensión no es posible esbozar un histórico sobre las hipótesis y estudios que llevaron a Mandelbrot a postular su teoría. Sin embargo, se remite al lector a algunos ensayos de divulgación llevados a cabo por el propio Mandelbrot como “¿Cuánto mide la costa de gran Bretaña?”.
4 El método de Box-counting o conteo de cajas permite el cálculo de la dimensión fractal de imágenes dividiendo estas en rejillas y comprobando en qué rejillas hay un fragmento de imagen. Se trata en realidad del mismo proceso que el explicado anteriormente, pero realizado automáticamente por un ordenador. Para más información ver: https://en.wikipedia.org/wiki/Box_counting
Bibliografía
Albert Samper y Blas. Análisis fractal de las catedrales góticas españolas. Informes de la Construcción. Vol. 66 (534). Herreras. 2014
Benoît Mandelbrot. 2009. La Geometría Fractal de la Naturaleza. [trad.] Josep Llosa. 3º Edición. Barcelona : Tusquets, 2009.
Boti, Alfredo Vera. 1994. La Catedral de Murcia y su plan director. Murcia: Colegio Oficial de Arquitectos de Murcia, 1994.
Eliezer Braun. 1996. Caos, fractales y cosas raras. Biblioteca digital del Instituto Latinoamericano de la Comunicación Educativa. [En línea] 1996. [Citado el: 23 de 10 de 2016.] Libro publicado online. http://bibliotecadigital.ilce.edu.mx/sites/ciencia/volumen3/ciencia3/150/htm/sec_5.htm.
